A thin rod AB of length a has variable mass per unit length ρ0(1+xa) where x is the distance measured from A and ρ0 is a constant.
Find the mass M of the rod.
The correct Answer is:3ρ0a2
Step by step video, text & image solution for A thin rod AB of length a has variable mass per unit length rho_(0) (1 + (x)/(a)) where x is the distance measured from A and rho_(0) is a constant. Find the mass M of the rod. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- 10 ROTATIONALBOOK - MOTIONCHAPTER - 10 ROTATIONALEXERCISE - Exercise - 4 (Level - I)
24 Videos
- 10 ROTATIONALBOOK - MOTIONCHAPTER - 10 ROTATIONALEXERCISE - Exercise - 4 (Level - II)
49 Videos
- 10 ROTATIONALBOOK - MOTIONCHAPTER - 10 ROTATIONALEXERCISE - Exercise - 3 (Level - I)
27 Videos
- ALTERNATING CURRENTBOOK - MOTIONCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - 4 (LEVEL - II)
14 Videos
Similar Questions
A thin rod AB of length a has variable mass per unit length P0(1+xa) where x is the distance measured from A and ρ0 is a constant.
Find the position of centre of mass of the rod.
View SolutionA thin rod AB of length a has variable mass per unit length ρ0(1+xa) where x is the distance measured from A and ρ0 is a constant.
Find moment of inertia of the rod about an axis passing through A and perpendicular to AB.
View Solution
Knowledge Check
A uniform thin rod AB of length L has linear mass density μ(x)=a+bxL, where x is measured from A. If the CM of the rod lies at a distance of (712L) from A, then a and b are related as :_
A2a=bB3a=2bCa=2bDa=bThe centre of mass of a non uniform rod of length L whoose mass per unit length varies asp=kx2/L, (where k is a constant and x is the distance measured form one end) is at the following distances from the same end
A3L/4BL/4C2L/3DL/3A thin rectangular plate with sides of length 'a' and 'b' has mass per unit area varying as α=α0(xyab) where α0 is a constant. The co-ordinated of centre of mass of the plate is
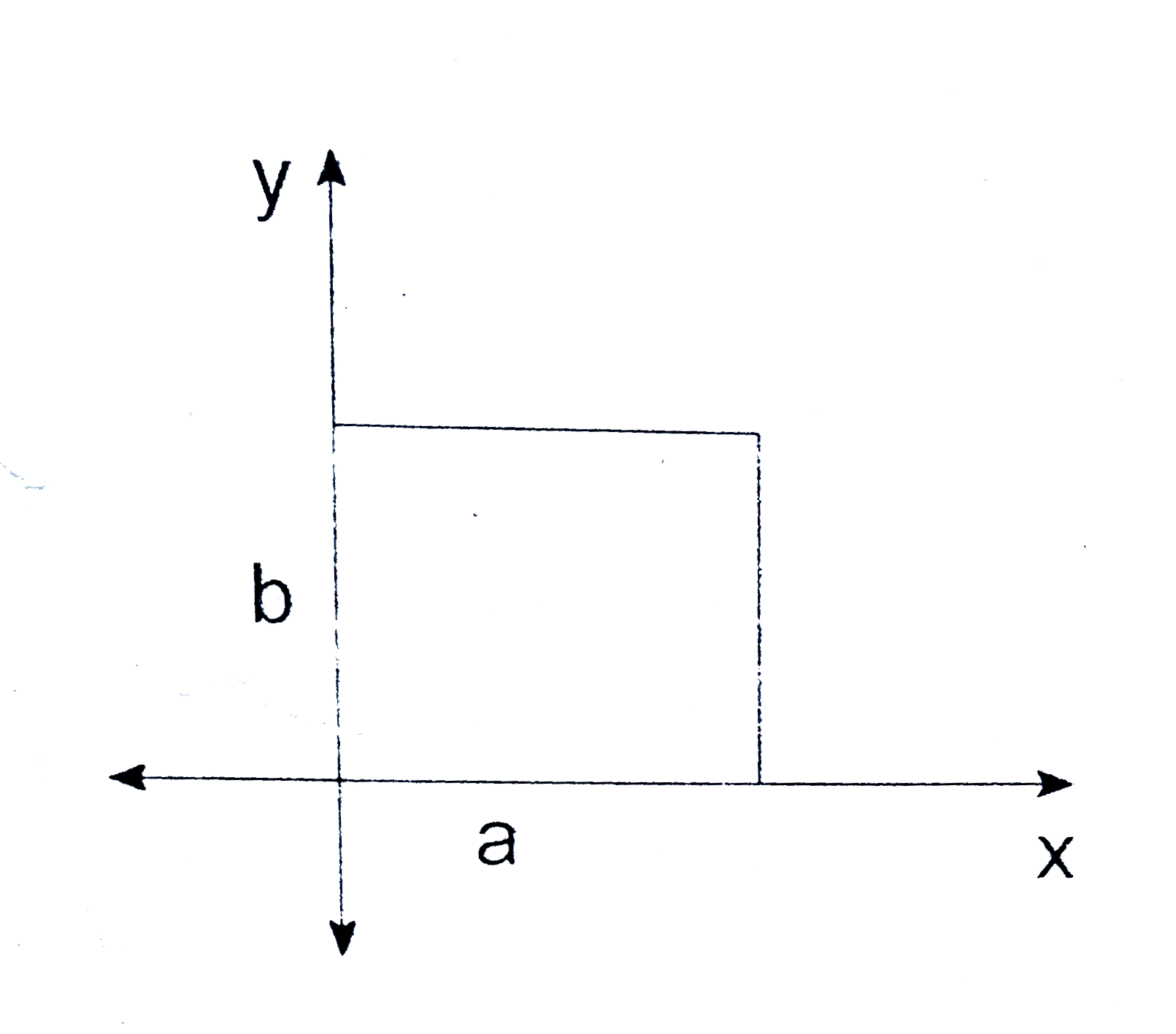 A(a3,b3)B(a2,b2)C(4a3,4b3)D(2a3,2b3)
A(a3,b3)B(a2,b2)C(4a3,4b3)D(2a3,2b3)
A thin rod AB of length a has variable mass per unit length ρ0(1+xa) where x is the distance measured from A and ρ0 is a constant.
Find minimum value of impulse P if B passes through a point vertically above A.
View SolutionA thin rod AB of length a has variable mass per unit length ρ0(1+xa) where x is the distance measured from A and ρ0 is a constant.
Rod is freely pivoted at A and is hanging in equilibrium when it is struck by a horizontal impulse of magnitude P at the point B. Find the angular velocity with which the rod begins to rotate.
View SolutionA rod of length L and cross section area A has variable density according to the relation ρ(x)=ρ0+kx for 0≤x≤L2 and ρ(x)=2x2 for L2≤x≤L where ρ0 and k are constants. Find the mass of the rod.
View SolutionA thin bar of length L has a mass per unit length λ, that increases linerarly with distance from one end. If its total mass is M and its mass per unit length at the lighter end is λ0, then the distance of the centre of mass from the lighter end is
View SolutionThe centre of mass of a, non uniform rod of length L whose mass per unit length p varies as p =kx2Lwhere k: is a constant and x is the distance of any point from one end, is (from the same end):
View Solution
