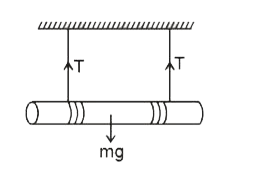
A cylinder of mass m is suspended through two strings wrapped around it as shwon in figure . Find (a). the tension T in the string and (b). the speed o the cylinder as it falls through a distance h.

The portion of the strings between ceiling and cylinder are at rest. Hence the points of the cylinder where the strings leave it are at rest also. The cylinder is thus rolling without slipping on the strings. Suppose the centre of cylinder falls with an acceleration a. The angular acceleration of cylinder about its axis given by
α=aR ...(i)
as the cylinder does not slip over the strings.
The equation of motion for the centre of mass of cylinder is
Mg - 2T = Ma
and for the motion about the centre of mass it is
2T.R=(MR22)α,whereI=MR22
2TR=MR22aR⇒2T=Ma2 ...(ii)
From (i) and (ii) on adding
Mg=Ma2+Ma,3a2=g
a=2g3
∴2T=M22g3⇒T=Mg6
As the centre of cylinder starts moving from rest, the velocity after it has fallen a height h is given by
v2=2[2g3]horv=√4gh3
Topper's Solved these Questions
Similar Questions
Knowledge Check
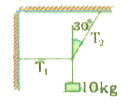
A block of mass 10 kg is suspended by three strings as shown in figure . Tension T2 is
 A100NB100√3NC√3×100ND50√3N
A100NB100√3NC√3×100ND50√3NA uniform rod of length l and mass M is suspended on two vertical inextensible string as shown in figure. Then tension T in the left string at the instant, when right string snaps is?
 AT=MgBT=Mg2CT=Mg4DT=zero
AT=MgBT=Mg2CT=Mg4DT=zeroA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
A√TlmB√2TlmC√3TlmD√Tml
A block of mass M si suspended by two strings angles θ1 and θ2 with the horizontal. Find the tensions in the strings.

View SolutionA cylinder of mass m suspended by two strings wrapped around the cylinder one near each end, the free ends of the string being attached to hooks on the ceiling, such that the length of the cylinder is horizontal. From the position of rest , the cylinder is allowed to roll down as suspension strings unwind , calculate
(a) The downward linear acceleration of the cylinder
(b) The tension in the strings
(c) The time dependence of the instantaneous power developed by gravity
View SolutionA 'block' of mass 10 kg is suspended with string as shown in figure. Find tension in the string. (g=10m/s2)

View SolutionA block of mass 30 kg is suspended by three string as shown in fig, Find the tension in each string.

View SolutionA uniform rod of length l and mass m is suspended by two vertical inextensible strings as shwon in figure. Then, tension in the left string when right string snape, si
View Solution