Each of the blocks shown in figure has mass 1 kg. The rear block moves with a speed of 2 m/s towards the front block kept at rest. The spring attached to the front block is light and has a spring constant 50 N/m. find the maximum compression of the spring.

EMaximum compression will take place when the blocks move with equal velocity. As no net external horizontal force acts on the system of the two blocks, the total linear momentum will remain constant. If V is the common speed at maximum compression, we have,
or,
Initial kinetic energy .
Final kinetic energy
The kinetic energy lost is stored as the elastic energy in the spring.
Hence,
or, x = 0.2 m.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 1
71 Videos
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 2 (Level-I)
40 Videos
- Capacitance BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -4 LEVEL II
19 Videos
- CIRCULAR MOTIONBOOK - MOTIONCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE - 4
16 Videos
Similar Questions
A block of mass 2 kg is moving on a frictionless horizontal surface with a velocity of 1m/s towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100N/m. Find the rnaximum compression of the spring
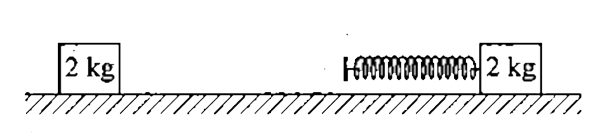
View SolutionA block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s figure towards abnother block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 The spring constant of the spring fixed at one end is 10 N/m. Find the maximum compression of the spring.

View Solution
Knowledge Check
A ball of mass m moving with speed v0 strikes a block of mass 3m kept at rest. The collision is completely inelastic . If k is spring constant , the maximum compression of the spring is
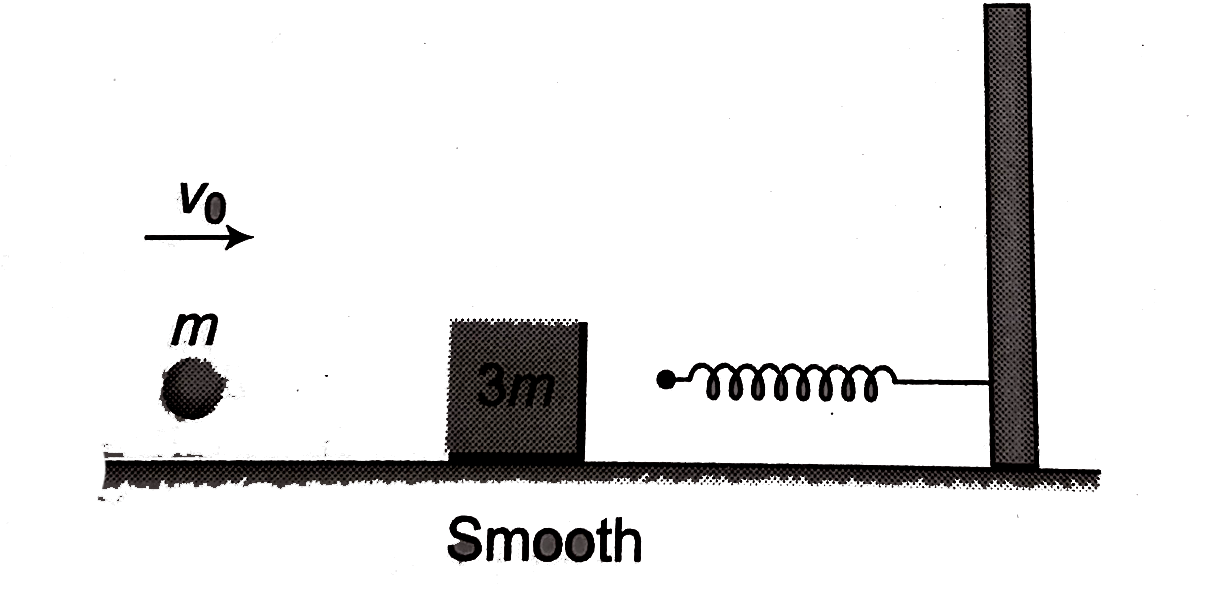 A√mv20kB√mv202kC√mv203kD√mv204k
A√mv20kB√mv202kC√mv203kD√mv204kTwo blocks of masses 1kg and 3kg are moving with velocities 2m/s and 1m/s , respectively , as shown. If the spring constant is 75N/m , the maximum compression of the spring is
 A5cmB2cmC3cmD4cm
A5cmB2cmC3cmD4cmA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
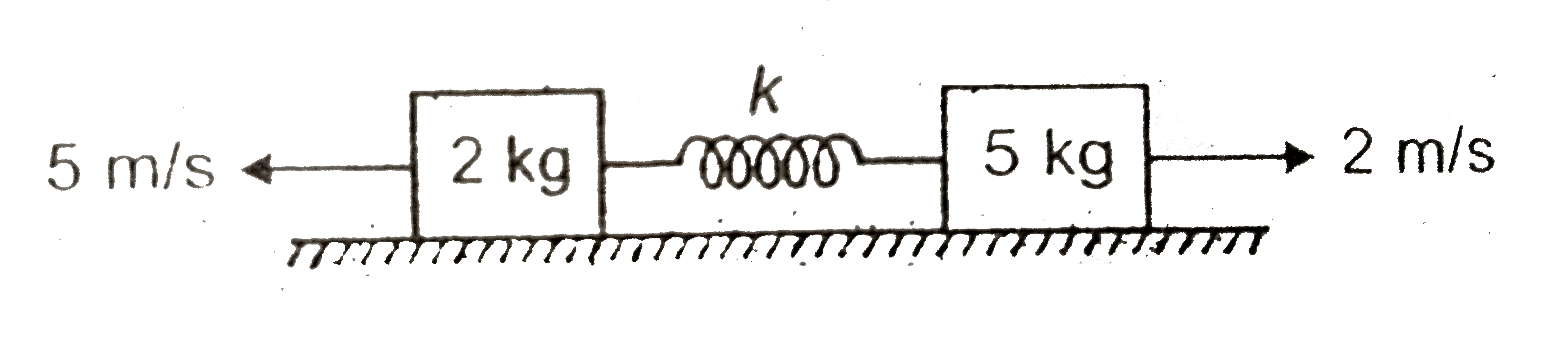
Two blocks of mass 2kg and 5kg are given speed as shown in the figure. System is lying on a frictionless surface and the blocks are connected by a massless spring if spring constant 35Nm. Find the maximum compression in the spring.
View SolutionThe block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m

View SolutionA block of mass m is connected to another block of mass M by a massless spring of spring constant k. the blocks are kept of a smooth horizontal plane and are at rest. The spring is unstretched when a constant force F starts acting on the block of mass M of pull it. Find the maximum extension of the spring

View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionBlock of mass m is pushed towards a horizontal spring as shown in figure , with initial speed u .

Spring constant of the spring is K and floor is smooth . Calculate maximum possible compression of the spring .
View Solution
