solid sphere of radius r is gently placed on a rough horizontal ground with an initial angular speed ω0 and no linear velocity. If the coefficient of friction is μ, find the time t when the slipping stops. in addition state the linear velocity v and angular velocity ω at the end of slipping
27rω0μg
37rωA0μg
37rω0μg
rω0μg
The correct Answer is:A
Step by step video, text & image solution for solid sphere of radius r is gently placed on a rough horizontal ground with an initial angular speed omega_(0) and no linear velocity. If the coefficient of friction is mu, find the time t when the slipping stops. in addition state the linear velocity v and angular velocity omega at the end of slipping by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.

View SolutionA disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View Solution
Knowledge Check
Relation between Linear velocity (v) and Angular velocity (ω)
Av=rωBω=vωCr=vωDv=ωrA disc of radius R rolls on a horizontal ground with linear acceleration a and angular acceleration α as shown in Fig. The magnitude of acceleration of point P as shown in the figure at an instant when its linear velocity is v and angular velocity is ω will be a
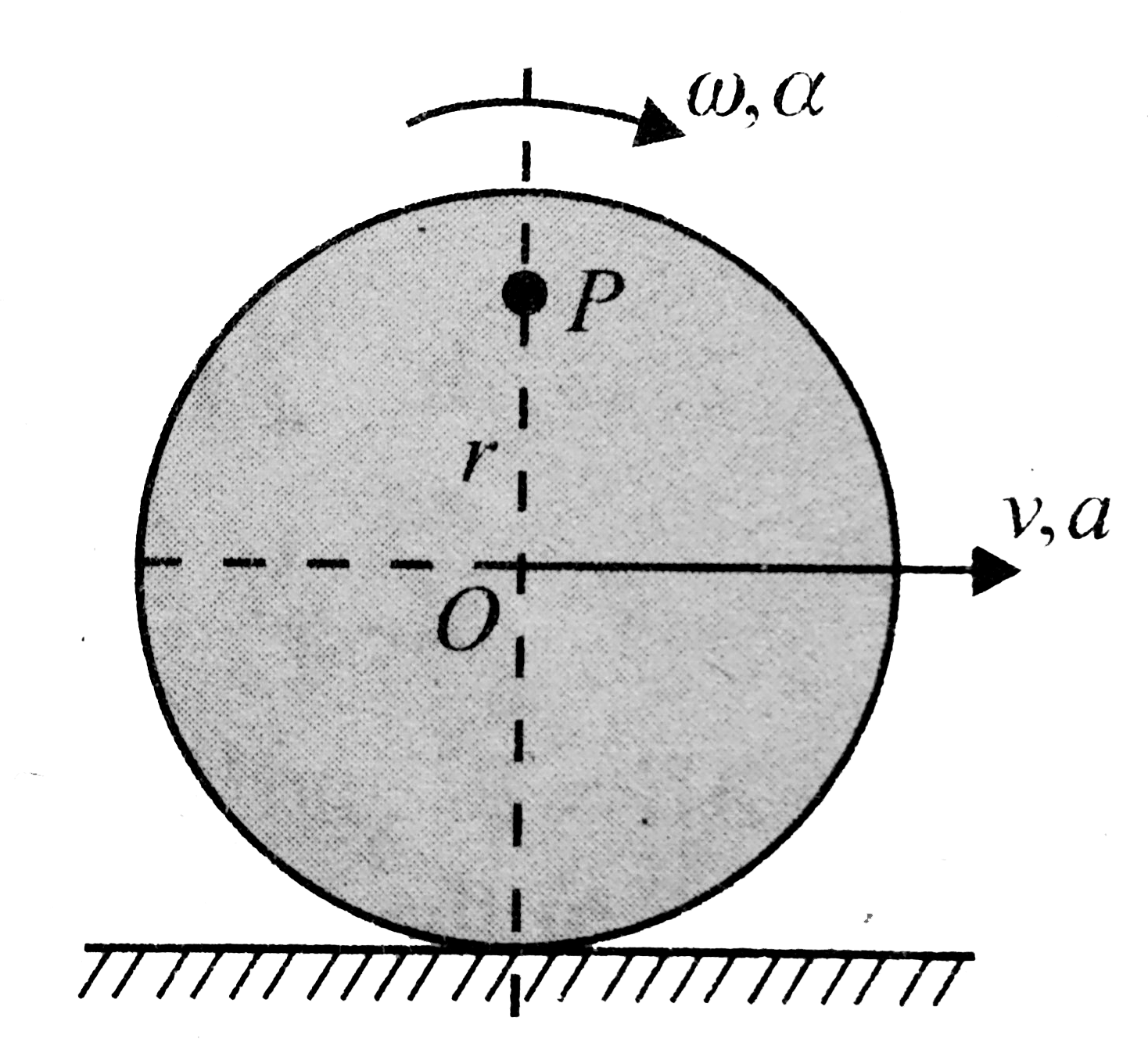 A√(a+rα)2+(rω2)2BarRC√r2α2+r2ω4Drα
A√(a+rα)2+(rω2)2BarRC√r2α2+r2ω4DrαThe correct relation between linear velocity →v and angular velocity →ω of a particle is
A→v=→ω×→rB→ω=→v×→rC→ω=→r×→vD→v=→r×→ω
A solid sphere is projected along an inclined plane according to diagram. If coefficient of friction is μ=0.5 and radius R, then find
(a) Time when linear velocity becomes zero
(b) Angular velocity at that instant

View Solution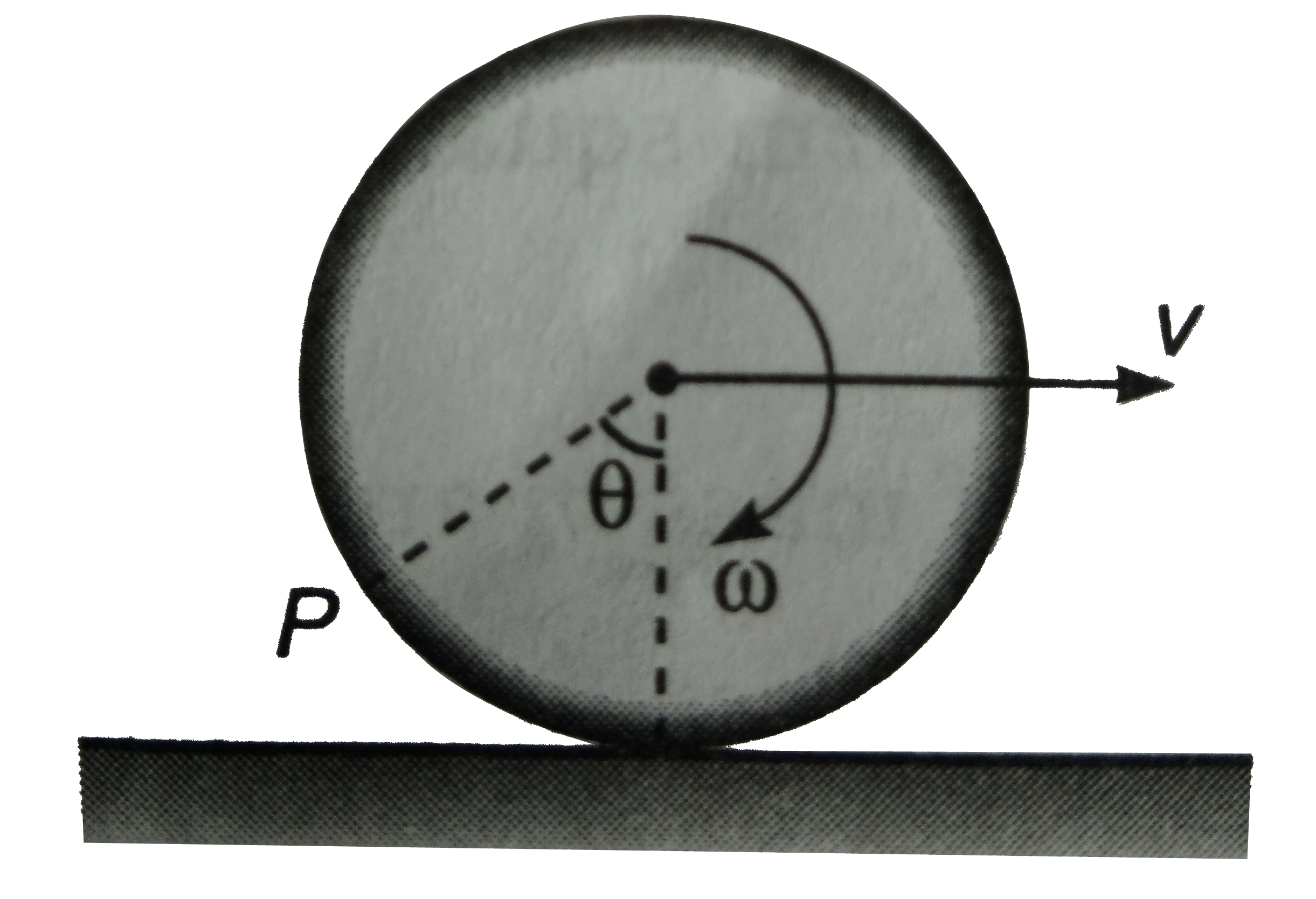
A ring of radius R rolls on a horizontal ground with linear speed v and angular speed ω. For what value of θ the velocity of point P is in vertical direction (v<Rω).
View SolutionA hollow sphere of radius r is rotating about a horizontal axis at some angular speed ω0. It is gently lowered to ground and the coefficient of friction between sphere and the ground is μ.How far does the sphere move before it starts pure rolling?
View SolutionA uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity V and angular velocity ω=(V=ωr). The sphere collides with a sharp edge on the wall as shown in Fig. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the sphere just after the collision is equal to
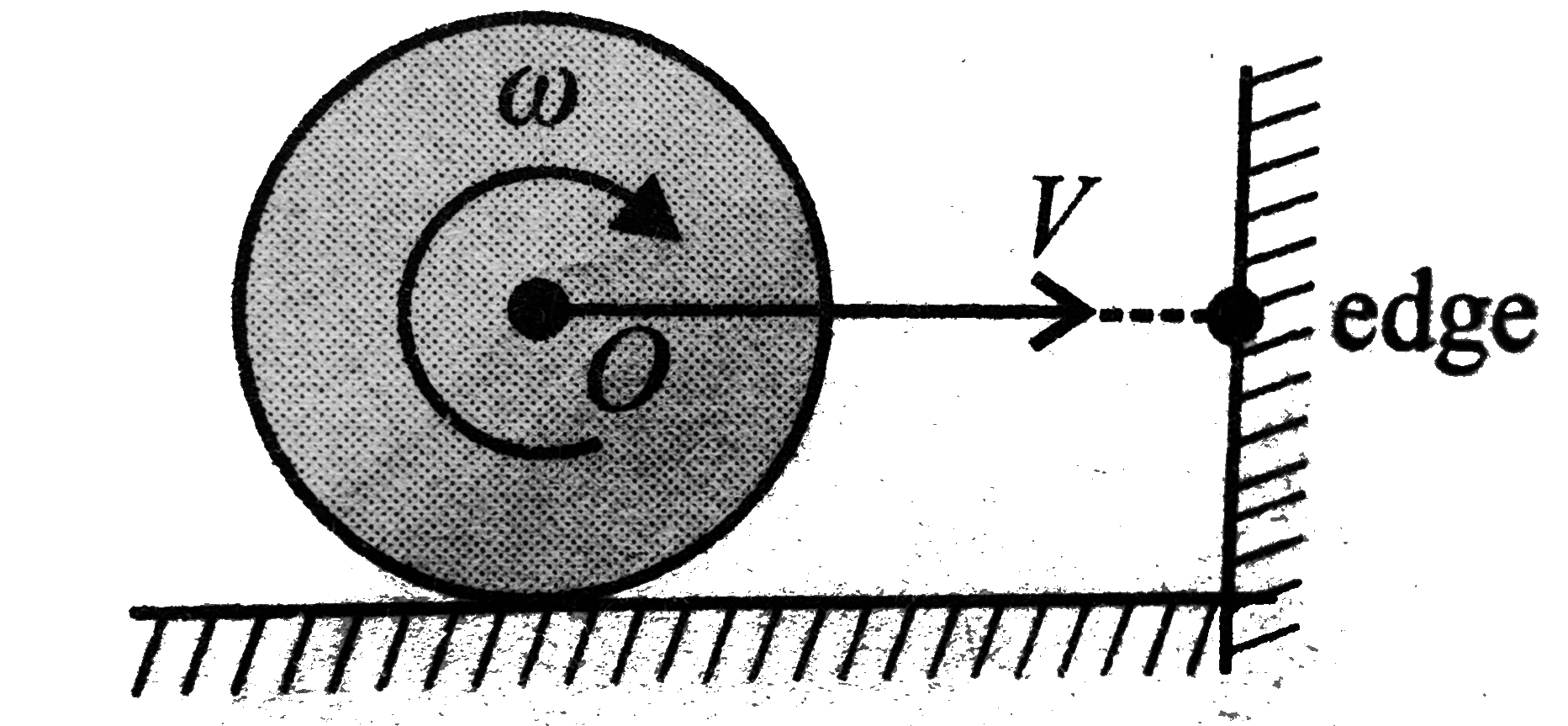
View SolutionA ring of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is μk. The time after it starts rolling is.
View Solution
