A cylindrical piece of cork of base area A and height h floats in a liquid of density ρ1. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hρρ1g
Say, inertially in equilibrium , y height of cylinder is inside the liquid . Then , weight of the cylinder =upthrust due to liquid displaced
∴Ahρg=Ayρg
when the corck cylinder is depressed slightly by Δy and realsed, a restoring force, equal to additional upthrust, acts on it. the restoring force is
F=A(y+Δy)ρlg−Ayρ1g−Ayρ1g=Aρ1gΔy
∴acceleration , a=Fm=Aρ1gΔyAhρ=ρ1ghρ.Δy and the acceleration is directed in the direction opposite to Δy, obviously as a∝−Detlay, the motion of cork cylinder is SHM, whose time period is given by
T=2π√displacementacceleration
=(2π√Δya)
=2π√hρρ1g
Topper's Solved these Questions
Similar Questions
A cylidrical wooden piece of cork floats in a liquid of density σ. The cork is depressed slightly and released. Show that the cork will oscillate up and down simple harmonicaly with a period.
T=2π√ρhσg, where ρ is the density of the cork.
View SolutionA block of ice with an area A and a height h floats in water of density ρ0. What work should be performed to submerge the ice block completely into water if density of ice is ρ1 ?
View Solution
Knowledge Check
A solid cube of side a and density ρ0 floats on the surface of a liquid of density ρ. If the cube is slightly pushed downward, then it oscillates simple harmonically with a period of
A2π√ρ0ρagB2π√ρρ0agC2π ⎷a(1−ρρ0)gD2π ⎷a(1+ρρ0)gA cylindrical of wood (density =600kgm−3) of base area 30cm2 and height 54cm, floats in a liquid of density 900kg−3 The block is deapressed slightly and then released. The time period of the resulting oscillations of the block would be equal to that of a simple pendulum of length (nearly) :
A26cmB52cmC36cmD65cmA rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
AT∝√ρBT∝1√ACT∝1ρDT∝1√m
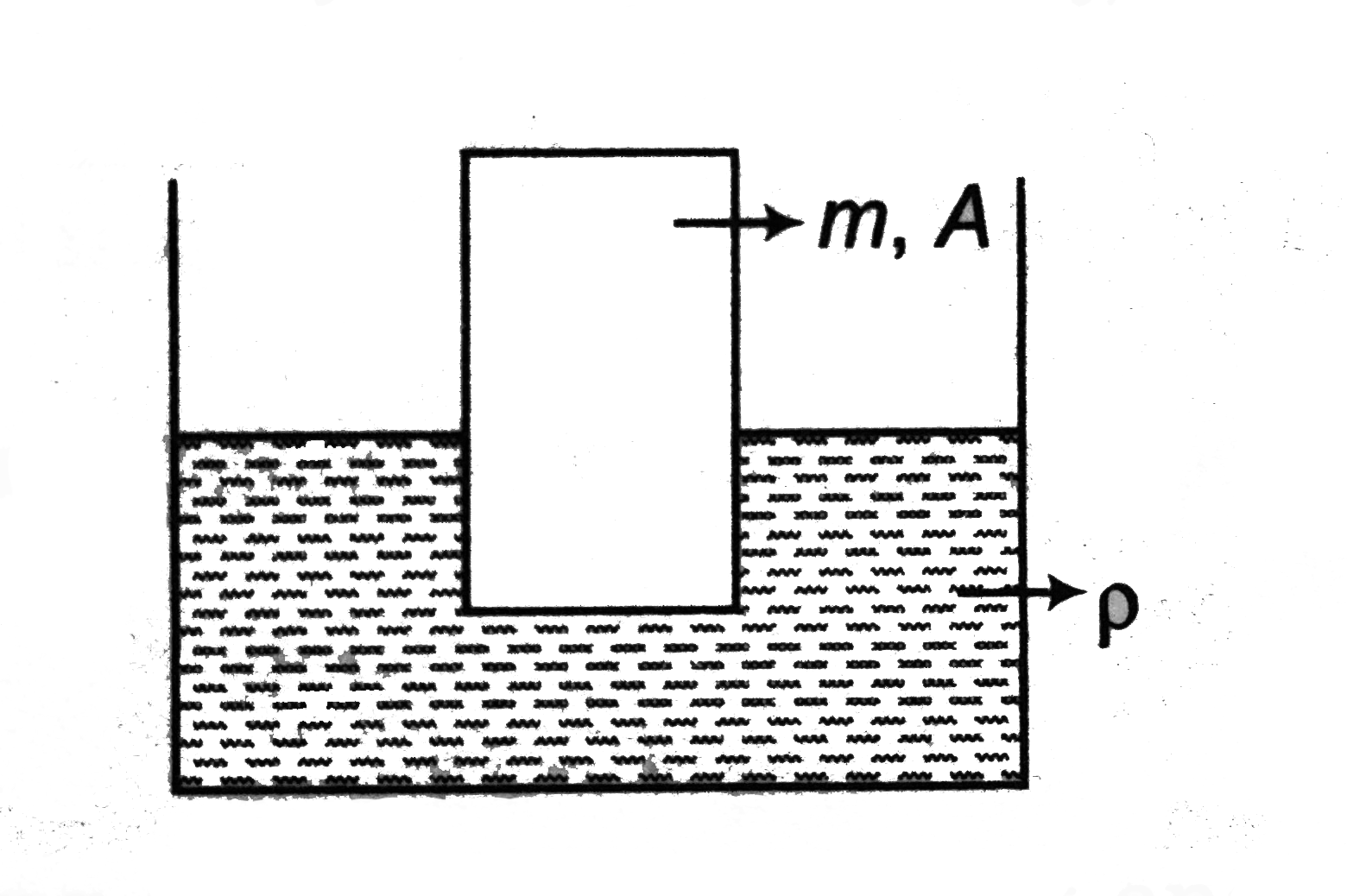
A plank of mass 'm' and area of cross - section A is floating in a non - viscous liquid of desity ρ. When displaced slightly from the mean position, it starts oscillating. Prove that oscillations are simple harmonic and find its time period.
View SolutionA cylinderical log of wood of height h and area of cross-section A floats in water. It is pressed and then released. Show that the log would execute S.H.M. with a tiem period.
T=2π√mAρg where m is mass of the body and ρ is density of the liquid.
View SolutionA cylindrical log of wood of height h and area of cross-section A floats in water. It is pressed and then released. Show that lon would execute SHM with a time period. T=2π√mApg where, m is mass of the body and p is density of the liquid.
View SolutionA wooden cube (density of wood ρ3 ') of side l 'floats in a liquid of density ' ρ with its upper and lower surfaces horizontal. If the cube is pushed slightly down and released, it performs simple harmonic motion of period T. Then, T is equal to 2π√xlyg. Find (x+y).
View SolutionA vertical U tube contains a liquid of density ρ, length of the liquid in the tube is 2H. The liquid is displaced slightly and released. Show that the liquid will execute SHM. Also find its time period. Take liquid to be ideal.
View Solution
