Show that for a particle in linear S.H.M., the average kinetic energy over a period of oscillation equals the average potential energy over the same period.
Video Solution
Text Solution
Let the particle executing SHM starts oscillating from its mean position. Then displacement equation is
x=Asinωt ltbRgt ∴ Particle velocity, v=Aωcosωt
∴ Istantaneous K.E. K=12mv2=12mA2ω2cos2ωt
∴ Average value of K.E. over one complete cylce
Kav=1T∫T012mA2ω2cos2ωtdt=mA2ω22T∫T0cos2ωtdt
=mA2ω22T∫T0(1+cos2ωt)2dt
=mA2ω24T[t+sin2ωt2ω]T0 ltBrgt =mA2ω24T[(T−0)+(sin2ωt−sin02ω)]
=14mA2ω2
Again instanteous P.E. =12kx2=12mω2x2=12mω2A2sin2ωt
∴ average value P.E. over one complete cycle
Uav=1T∈T012mω2A2sin2ωt=mω2A22T∫T0sin2ωtdt
=mω2A22T∫T0(1−2cosωt)2dt
=mω2A24T[t−sin2ωt2ω]T0
=mω2A24T[(T−0)−(sin2ωt−sin0)2ω]
=14mω2A2......(ii)
Simple comparison (i) and (ii) , shows that
Kav=Uav=14mω2A2
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
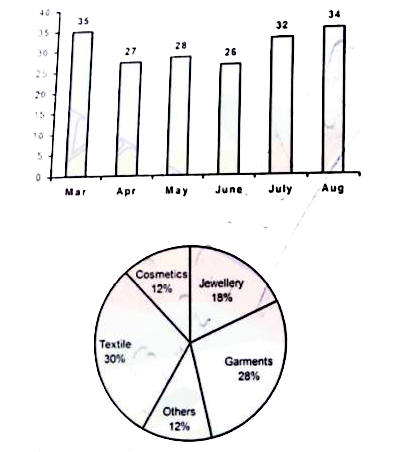
What is the average import of textiles indstry over the period ?A22.32billionB24.32 billionC21.84billionDNone of these - Question 2 - Select One
Average kinetic energy of molecules is
Adirectly proportional to square root of temperature .Bdirectly proportional to absolute temperature.Cindependent of absolute temperature.Dinversely proportional to absolute temperature - Question 3 - Select One
A table below shows the production and imports of circle oil (in '000 tonnes). Domestic production of crude oil is total of on-share and off-shore production, which is supplemented by imports to meet the total demand of crude oil in the country.

What is the average of total demand of crude oil over the period ?A185 million tonnesB52 million tonnesC18.5 million tonnesD35 million tonnes
The average acceleration over on period of oscialltion for a simple harmonic motion is
View SolutionThe force and acceleration in S.H.M. changes in direction over a period
View SolutionAverage kinetic energy of CO2 at 300 K is E. The average kinetic energy of N2 at the same temperature will be
View SolutionFor a particle executing S.H.M., the kinetic energy K is given K=K0cos2ωt. The maximum value of potential energy is:
View SolutionFor a particle performing a linear SHM the ratio of the frequency of oscillation and the frequency of kinetic energy is
View Solution

