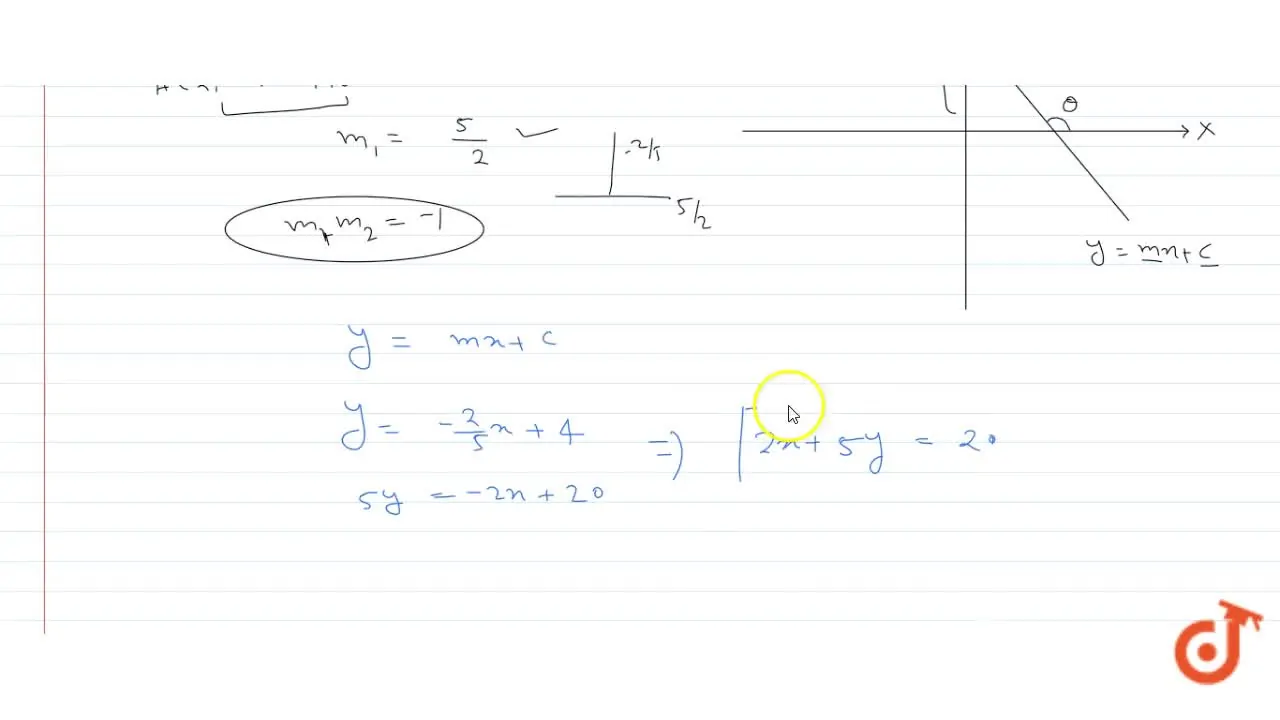
Find the equation of a line that has y - intercept 4 and is perpendicular to the line joining (2,−3)and(4,2).
3y=2x−7
y=23x−73
As m1=23,m2=32
Thus,y=−32x+4
2y+3x=8
for x int(a,0),
2(0)+3(a)=8
∴a=83
Related Playlists
Similar Questions
Find the equation of a line that has y - intercept 4 and is perpendicular to the line joining (2,−3)and(4,2).
View SolutionFind the equation of a line that has -y-intercept 4 and is a perpendicular to the line joining (2,−3) and (4,2).
View SolutionFind the equation of a straight line that has y-intercept 4 and is perpendicular to straight line joining (2,-3) and (4.2)
View SolutionFind the equation of the line that has y-intercept −3 and is perpendicular to the line 3x+5y=4.
View SolutionFind the equation of a line that x-intercept 3 and perpendicular to the line x−7y+5=0
View SolutionFind the equation of the line that has x-intercept-3 and which is perpendicular to the line 3x+5y=4
View SolutionFind the equation of a line has y-intercept is −4 and is parallel to the line joining (2,−5)and(1,2).
View SolutionFind the equaiton of the line that has y-intercept 4 and is parallel to the line 2x−3y=7.
View SolutionFind the equation of the the line which has x-intercept -8 and is perpendicular to the line x+4y-17=0.
View SolutionFind the equation of the line whose y-intercept is -3 and which is perpendicular to the line joining the points (-2,3) and (4,-5).
View Solution