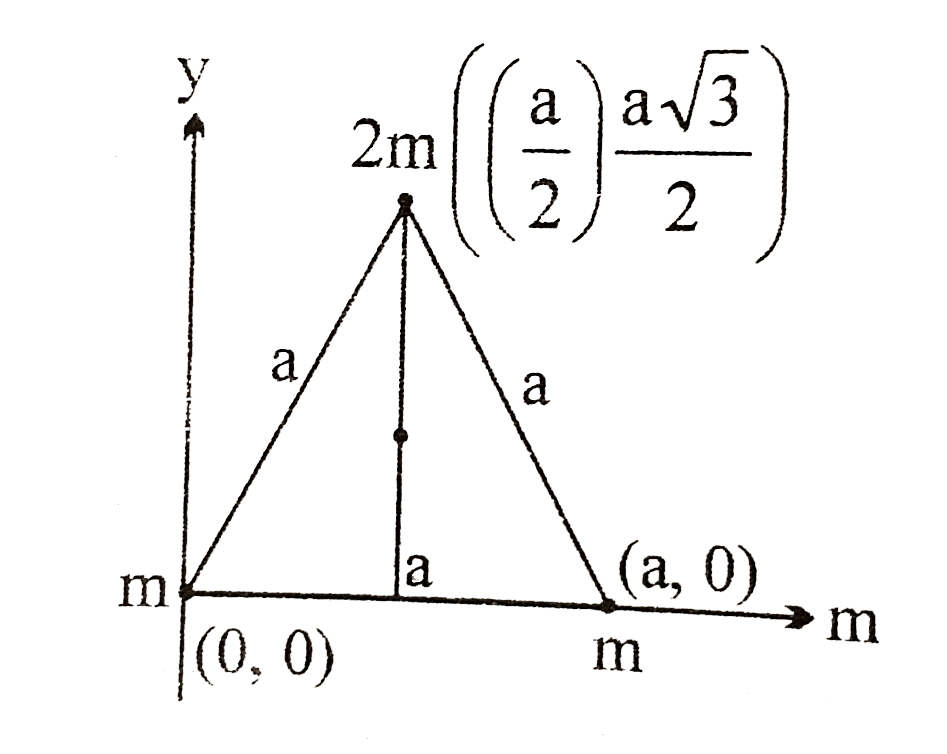Find the centre of mass of three particle at the vertices of an equilateral triangle. The masses of the particle are 100g,150g,and200g respectively. Each side of the equilateral triangle is 0.5m along.
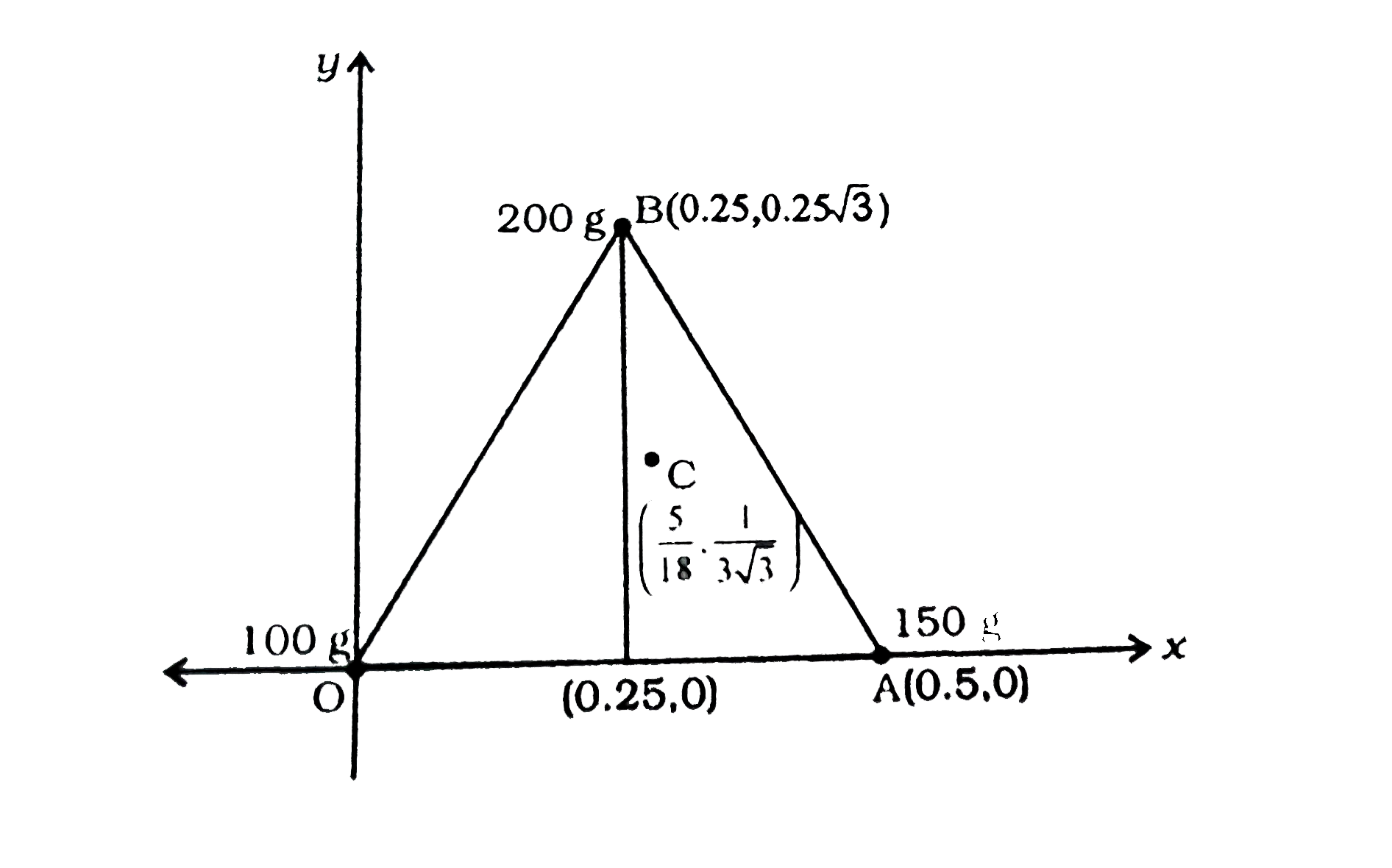
With the x-and y-axes chosen as shown in Fig. 7.9, the coordinates of points O, A and B forming the equilateral triangle are respectively (0,0), (0.5,0),(0.25,0.25√3). Let the masses 100 g, 150 and 200 g be located at O, A and B be respectively. Them, X=m1x1+m2x2+m3x3m1+m2+m3
=100(0)+150(0.5)+200(0.25)gm(100+150+200)g
=75+50450m=125450m=518m
Y=100(0)+150(0)+200(0.25√3)450g
=50√3450m=√39m=13√3m
The centre of mass C is shown in the figure. Note that is it is not the geometric centre of the triangle OAB. Why ?
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - NCERTCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISE
33 Videos
- PHYSICAL WORLD BOOK - NCERTCHAPTER - PHYSICAL WORLD EXERCISE - EXERCISE
16 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERTCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXERCISE
22 Videos
Similar Questions
Knowledge Check
The centre of masses of three particles of mass m1=m2=m3=1 kg at the corners of an equilateral triangle of side 1 m will be -
A0.50m, 0.29mB0.43m, 0.50mC0.25m, 0.25mD0.22m, 0.22mThree masses each of mass m are placed at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is
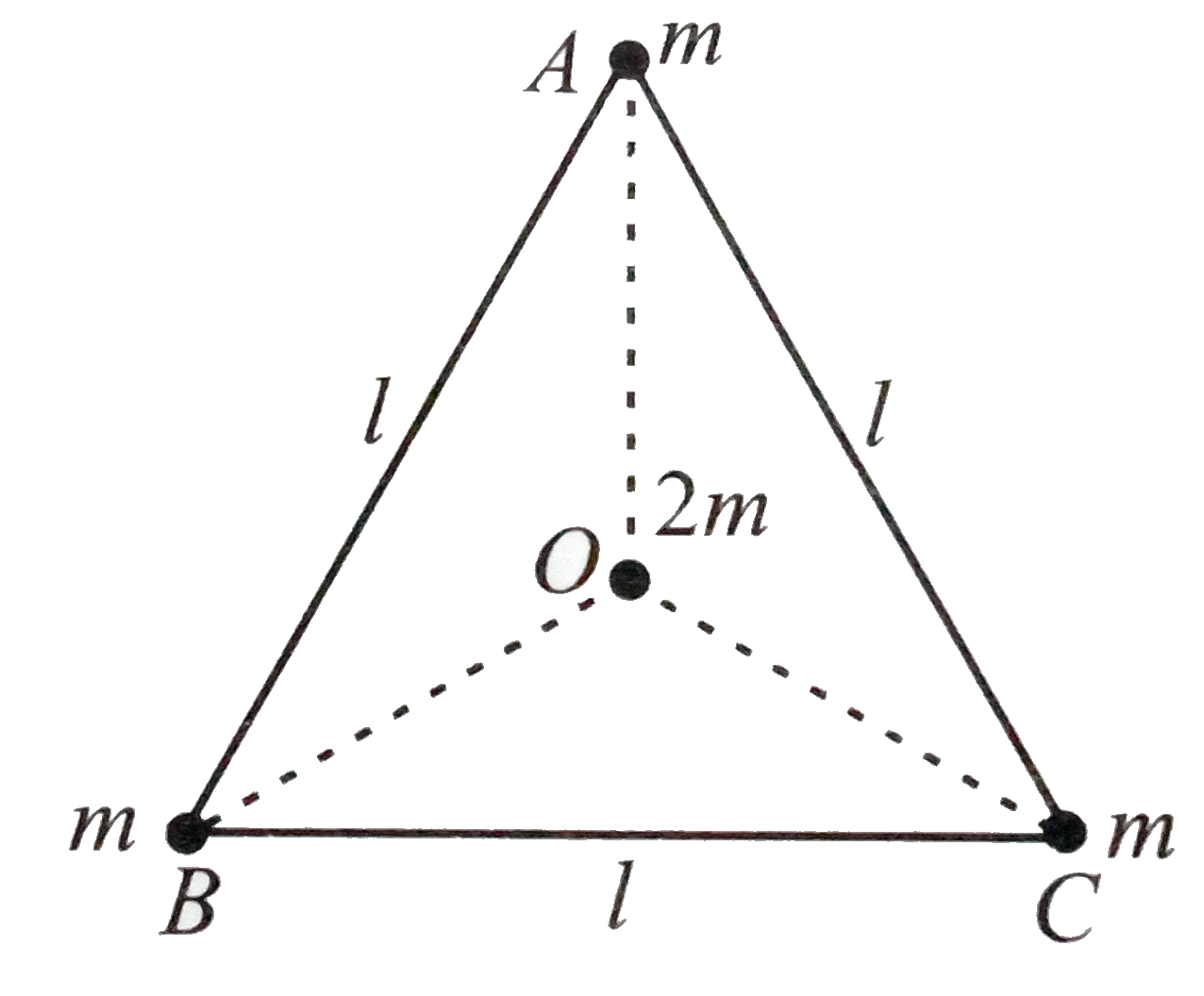 AzeroB3Gm2l2C5Gm2l2D7Gm2l2
AzeroB3Gm2l2C5Gm2l2D7Gm2l2Three particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
A−3GMLB−√3GMLC−3√3GMLD−GM3√3L
Three identical point objects each of mass m are placed at the vertices of an equilateral triange of side l. What is the gravitational potential at the centre of the equilateral triangle due to the point masses?
View SolutionFind the perimeter of an equilateral triangle with each side measuring 5.8 cm.
View SolutionFind the PE of three objects of masses 1kg,2kg and 3kg placed at the three vertices of an equilateral triangle of side 50cm ?
View SolutionThree particles, each of mass m are placed at the vertices of an equilateral triangle of side a. What are the gravitation field and gravitational potential at the centroid of the triangle.
View SolutionThree particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
View Solution