
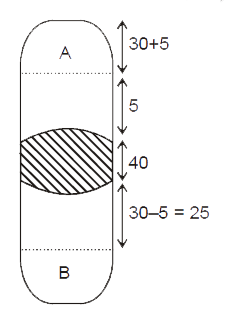
Assume constant temperature if the tube is changed to vertical position and the pallet comes down by 5 cm then find out P0
For upper part
P1V1=P0V0
P135A=P030A
P1=3035P0…(i)
For lower part
P2V2=P0V0
P030A=P225A
P2=3025P0…(ii)
Again
P1+40=P2...(iii)
From (i) and (ii)
3025P0+40=3025P0
Topper's Solved these Questions
- HEAT-2 Book:MOTIONChapter:HEAT-2 Exercise:EXERCISE-1
Explore 40 Videos
- HEAT-2 Book:MOTIONChapter:HEAT-2 Exercise:EXERCISE-2 (LEVEL-I)
Explore 24 Videos
- HEAT TRANSFER & THERMAL EXPANSION Book:MOTIONChapter:HEAT TRANSFER & THERMAL EXPANSION Exercise:Exercise - 3 Section-B
Explore 19 Videos
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBook:MOTIONChapter:HYDROSTATIC, FLUID MECHANICS & VISCOSITYExercise:EXERCISE -3 (SECTION-B) PREVIOUS YEAR PROBLEM
Explore 7 Videos
Similar Questions
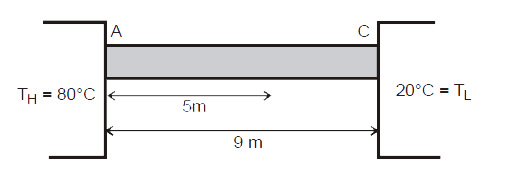
Find out the temperature at distance 5 m.
View SolutionTwo arms of a U-tube have unequal diameters d1=1.0mm and d2=1.0cm. If water (surface tension 7×10−2N/m) is poured into the tube held in the vertical position, find the difference of level of water in the U-tube . Assume the angle of contact to be zero.
View Solution
Knowledge Check
Water rises to a height of 5 cm when a narrow glass tube is dipped vertically in it . If the tube is inclined at 60∘ to the vertical , then the rise of water in the capillary tube will be
A5 cmB10 cmC7.5 cmD2.5 cm
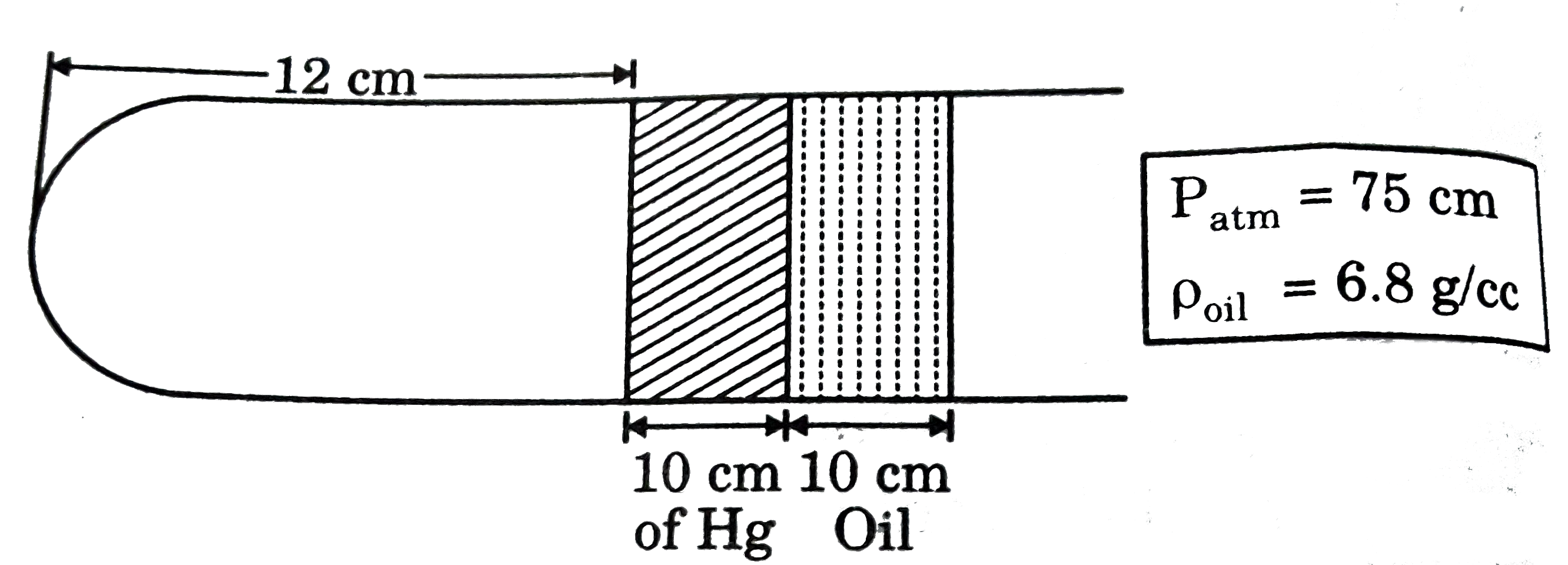
If above tube is held vertical with open end upward then find the length of air column (in cm).
View SolutionAt constant temperature, if vol. of gas decrease by 5% then what will be to change in pressure.
View SolutionIn given figure, A uniform cylindrical tube closed at one end, contains a pallet of mercury 5cm long. When the tube is kept verticaly with the closed end downward, the length of the air column trapped is 30cm. Now the tube is inverted so that the closed end goes up find the new length of the air column trapped. atmospheric pressure =75cm of mercury. (Assume temperature remains constant in this process)

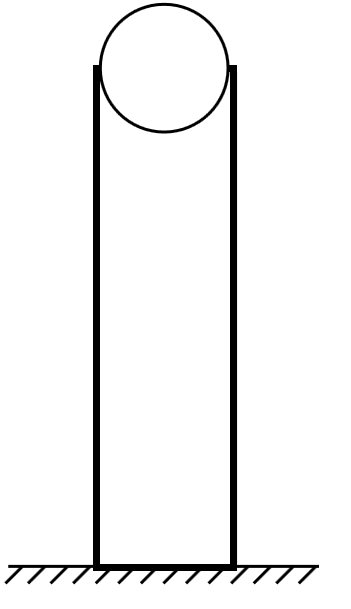
View SolutionThere is a long vertical tube of radius r containing air at atmospheric pressure. A steel ball is held at the mouth of the tube and dropped. The ball has radius r and it just fits inside the tube. The tube wall is perfectly smooth and no air can leak from the tube as the ball falls inside it. The ball falls through half the length of the tube before coming to rest. Assume that wall of the tube is perfectly conducting and temperature of the air inside the tube remains constant. Density of steel is d and atmospheric pressure is P0 and take L>>r. Take air to be an ideal gas.
(a) Find the radius (r) of the tube.
(b) At what depth from the top of the tube the ball will be in equilibrium?
View SolutionA narrow tube of length l and radius r is sealed at one end. Its open end is brought in contact with the surface of water while the tube is held vertical. The water rises to a height h in the tube. The contact angle of water with the tube wall is θ, density of water is ρ and the atmospheric pressure is Po. Find the surface tension of the liquid. Assume that the temperature of air inside the tube remains constant and the volume of the meniscus is negligible.
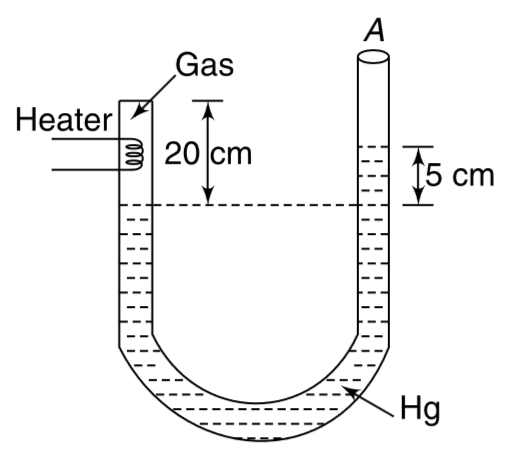
View SolutionOne end of an insulating U tube is sealed using insulating material. A mono atomic gas at temperature 300 K occupies 20 cm length of the tube as shown. The level of mercury on two sides of the tube differ by 5 cm. The other end of the tube is open to atmosphere. Area of cross section of the tube is uniform and is equal to 0.01m2. The gas in the tube is heated by an electric heater so as to raise its temperature to 562.5 K. Assume that no heat is conducted to mercury by the gas.
(a) Find the final length of the gas column.
(b) Find the amount of heat supplied by the heater to the gas.
View SolutionTwo vertical cylinders are connected by a small tube at the bottom. It contains a gas at constant temperature . Initially the pistons are located at the same height. The diameters of the two cylinders are different . Outside the cylinder the space is vaccum . Gravitational acceleration is h,h0=20cm,m1=2kgandm2=1kg. The pistons are initially in equilibrium. If the masses of the piston are interchanged find the separation between the two pistons when they are again in equilibrium. Assume constant temperature .
_E01_299_Q01.png)
View Solution

