Find the new length of gas column in tube if tube is rotated at an angle 60∘ as shown. (Assume constant temperature)
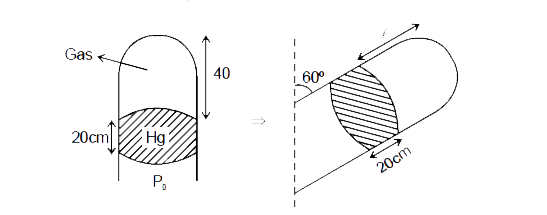
Pgas=75−20=55
[P+20cos60=75
P1V1=P2V2
2P+20=150
55×40×A=65×l×A
2P=130
l=55×4065
P=65]
Topper's Solved these Questions
- HEAT-2 Book:MOTIONChapter:HEAT-2 Exercise:EXERCISE-1
Explore 40 Videos
- HEAT-2 Book:MOTIONChapter:HEAT-2 Exercise:EXERCISE-2 (LEVEL-I)
Explore 24 Videos
- HEAT TRANSFER & THERMAL EXPANSION Book:MOTIONChapter:HEAT TRANSFER & THERMAL EXPANSION Exercise:Exercise - 3 Section-B
Explore 19 Videos
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBook:MOTIONChapter:HYDROSTATIC, FLUID MECHANICS & VISCOSITYExercise:EXERCISE -3 (SECTION-B) PREVIOUS YEAR PROBLEM
Explore 7 Videos
Similar Questions
Find the new length of gas column in tube if tube is inverted (Assume temperature is constant)

View SolutionAn ideal gas is trapped between a mercury column and the closed lower end of a narrow vertical tube of uniform bore. The upper end of the tube is open to atmosphere (atmospheric pressure = 76 cm of Hg). The length of mercury and the trapped gas columns are 20 cm and 43 cm respectively. What will be the length of the gas column when the tube is titled slowly at constant temperature in a vertical plane through an angle of 60∘ ?
View Solution
Knowledge Check
A tuning fork is used to produce resonance in glass tuve. The length of the air column in the tube can be adjusted by a variable piston. At room temperature of 27∘C two succesive resonance are produced at 20 cm and 73 cm column length. If the frequency of the tuning fork is 320 Hz. the velocity of sound is air at 27∘C is
A350 m/sB339 m/sC330 m/sD350 m/sA uniform tube is shown in figure, Which is open at one en and closed at the other . To enclose a column of air inside the tube, a pellet of mercury is introduced If the length of air column at 27∘C is 18 cm, at what temperature its length will be 21.6?
 A87∘CB91∘CC85∘CD97∘C
A87∘CB91∘CC85∘CD97∘CIn an experiment a capillary tube is kept vertical , then water rises up in the tube upt 3mm height . When the tube is fitted at an angle of 60∘ with verical , what should be the height of water rise
A6 mmB4 mmC3 mmDNone of these
An ideal gas is trapped between a mercury column and the closed lower end of a narrow vertical tube of uniform bore. The upper end of the tube is open to atmosphere (atmospheric pressure = 76 cm of Hg). The length of mercury and the trapped gas columns are 20 cm and 43 cm respectively. What will be the length of the gas column when the tube is titled slowly at constant temperature in a vertical plane through an angle of 60∘ ?
View SolutionCalculate the length of mercury column in a barometer tube which is inclined at an angle of 45∘ with horizontal direction if the atmospheric pressure is 75 cm of mercury.
View SolutionIn given figure, A uniform cylindrical tube closed at one end, contains a pallet of mercury 5cm long. When the tube is kept verticaly with the closed end downward, the length of the air column trapped is 30cm. Now the tube is inverted so that the closed end goes up find the new length of the air column trapped. atmospheric pressure =75cm of mercury. (Assume temperature remains constant in this process)

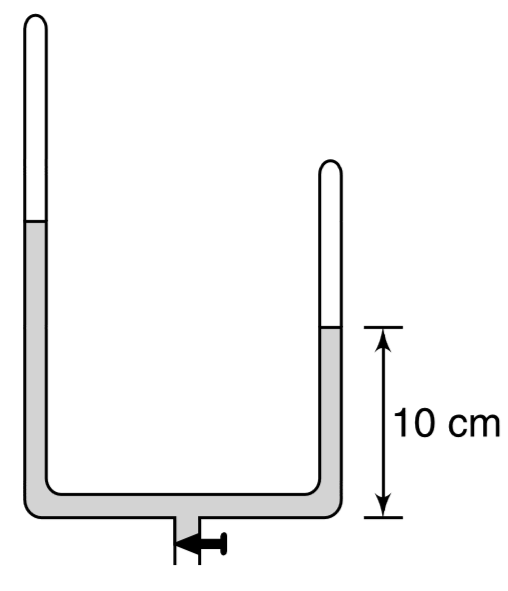
View SolutionA U shaped tube has two arms of equal cross section and lengths l1=80 cm and l2=40 cm. The open ends are sealed with air in the tube at a pressure of 80 cm of mercury. Some mercury is now introduced in the tube through a stopcock connected at the bottom (the air is not allowed to leak out). In steady condition the length of mercury column in the shorter arm was found to be 10 cm. Find the length of the mercury column in the longer arm. Neglect the volume of the part of the tube connecting two arms and assume that the temperature is constant.
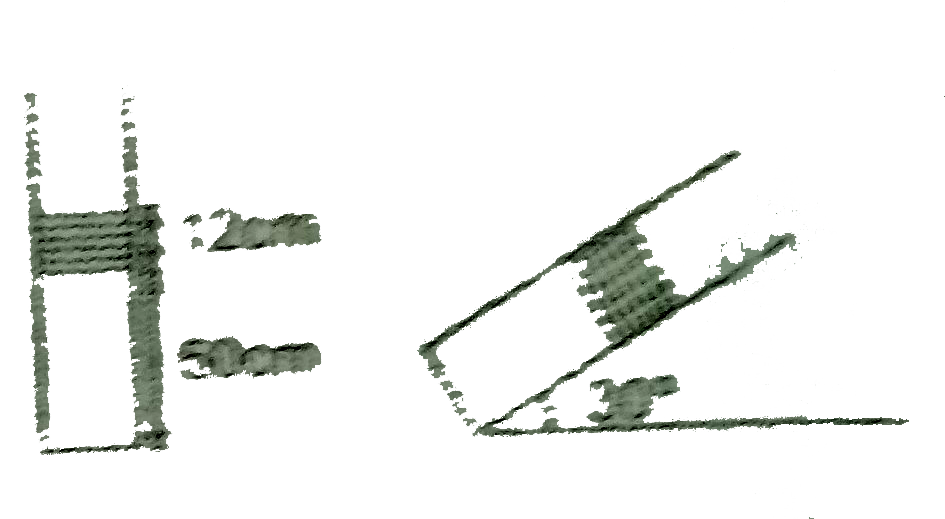
View SolutionIn given figure, an ideal gas is trapped between a mercury column and the closed end of a uniform vertical tube. The upper end of the tube is open to the atmosphere. Initially the lengths of the mercury column and the trapped air colume are 12cm and 50cm respectively. when the tube is titted solwly in a vertical plane through an angle of 30∘ with horizontal then the new length of air colume is x41m. Find x. Assuming the temperature to remains constant. (Patm=76cmofHg)
View Solution

