A force F=-10x+2 acts on a particle of mass 0.1 kg where m is m and F is in newtons. If F is released from rest at x=0, find:
a. amplitude:
b. time period:
c. equation of motion.

Video Solution

Text Solution

Verified by Experts

(a) $\frac{11}{5}$ m (b) $\frac{π}{5}$ sec ( c) $x = 0.2 - \frac{11}{5} cos ω t$

Updated on:21/07/2023

A force $F = B e^{C t}$ acts on a particle whose mass is m and whose velocity is 0 at t = 0. It's terminal velocity is :
A $\frac{C}{m B}$
B $\frac{B}{m C}$
C $\frac{B C}{m}$
D $- \frac{B}{m C}$
Passage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
What it is the time period of periodic motion of particle.

A $4 (\sqrt{\frac{2 A m}{F}}$
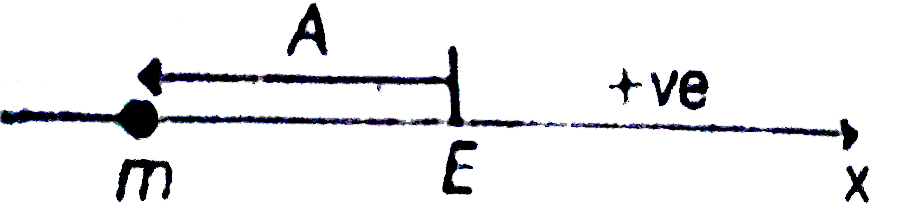B $2 (\sqrt{\frac{2 A m}{F}})$
C $(\sqrt{\frac{2 A m}{F}})$
DNone of these
A force $f = 10 + 2 x$ acts on a particle moving in straight line on x axis the work done by this force during a displacement from $x = 0$ and $x = 3 m$
A $13$ J
B $29$ J
C $39$ J
D $43$ J