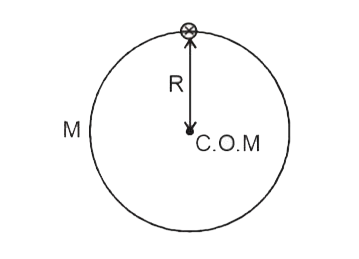
A ring is suspended at a point on its rim and it behaves as a second's pendulum when it oscillates such that its centre move in its own plane. The radius of the ring would be (g = π2)
Time period of second pendulum T = 2 cm.
T=2π√IMgd
Moment of inertia with respect to axis O
I=MR2+MR2=2MR2
the distance between centre of mass and the axis O
d= R
2=2π√2MR2MgR⇒R=0.5m
Topper's Solved these Questions
- SIMPLE HARONIC MOTION BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -1 ( SECTION-A )
8 Videos
- SIMPLE HARONIC MOTION BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -1 ( SECTION-B ) (Time per iod and angu larfrequency in SHM)
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - B Previous Year Problems | JEE MAIN
23 Videos
- SOUND WAVESBOOK - MOTIONCHAPTER - SOUND WAVESEXERCISE - Exercise - 3 (Section - B)
14 Videos
Similar Questions
Knowledge Check
A ring of diameter 2m oscillates as a compound pendulum about a horizontal axis passing through a point at its rim. It oscillates such that its centre move in a plane which is perpendicular to the plane of the ring. The equibvalent length of the simple pendulum is
A2mB4mC1.5mD3m
A uniform semicurcular ring having mass m and radius r is hanging at one of its ends freely as shown if Fig. The ring is slightly disturbed so the it oscillates in its own plane. The time period of oscillation of the ring isA2π ⎷rg(1+1π2)B2π ⎷rg(1+4π2)12C2π ⎷rg(1−2π2)12D2π ⎷2rg(1+4π)12A second's pendulum is mounted in a rocket. Its period of oscillation decreases when the rocket
AMoves up with uniform accelertionBMoves up with a uniform velocityCComes down with uniform accelerationDMoves round the earth in a geosterationary orbit.
A thin ring of radius R is made of a material of density ρand Young's modulus Y. If the ring is rotated about its centre in its own plane with angular velocity omega , find the small increases in its radius.
View SolutionA ring of mass 0.8 kg and radius 1m is hinged at a point on its periphery such that the hinge is at the same horizontal level as its centre. The ring in vertical plane and released. Find the force exerted (in N) by the hinge on the ring just after the release.
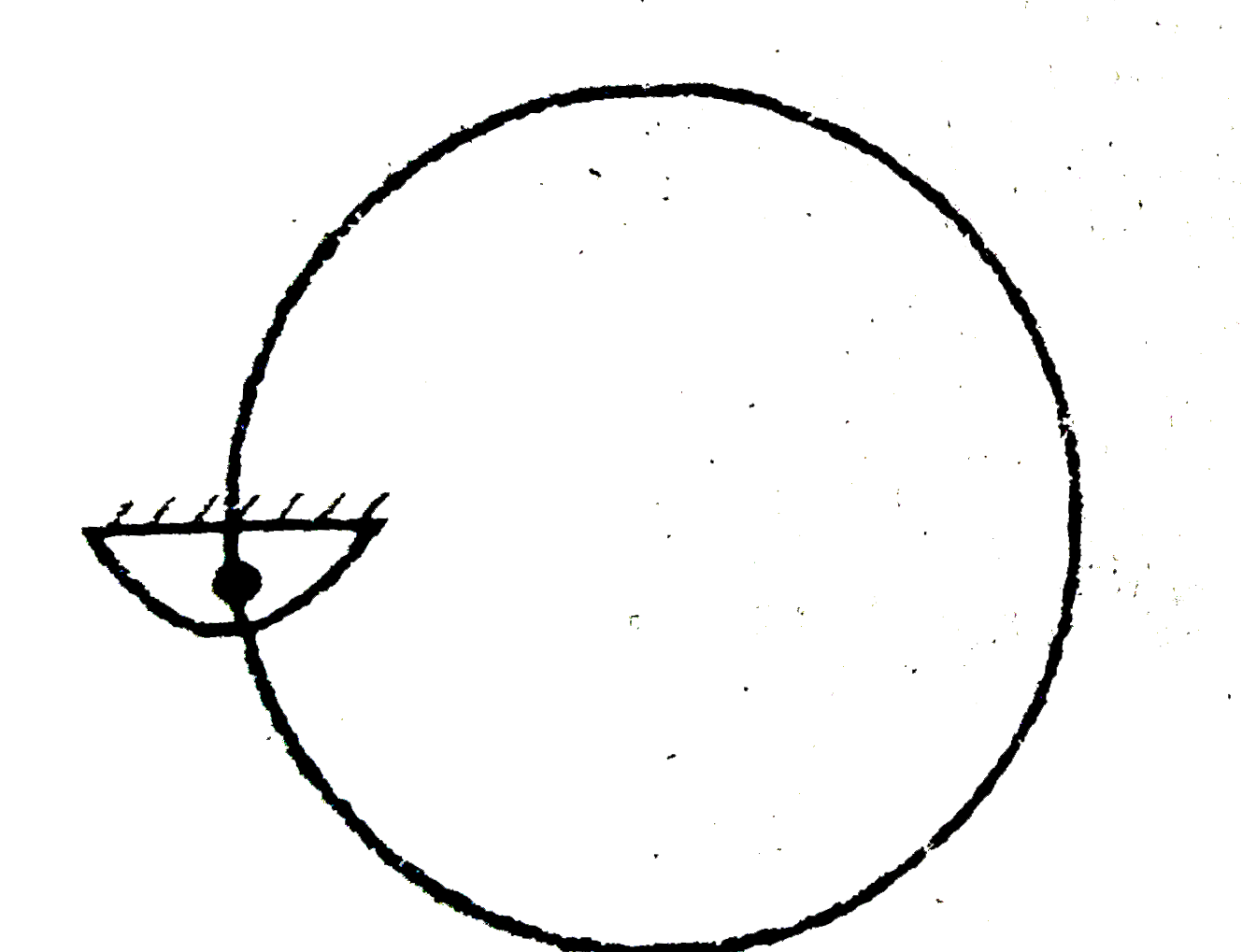
View SolutionA ring of the radius r is suspended from a point on its circumference. If the ring is made to oscillate in the plane of the figure, then the angular frequency of these small oscillations is
View SolutionThe moment of inertia of semicircular ring about its centre is
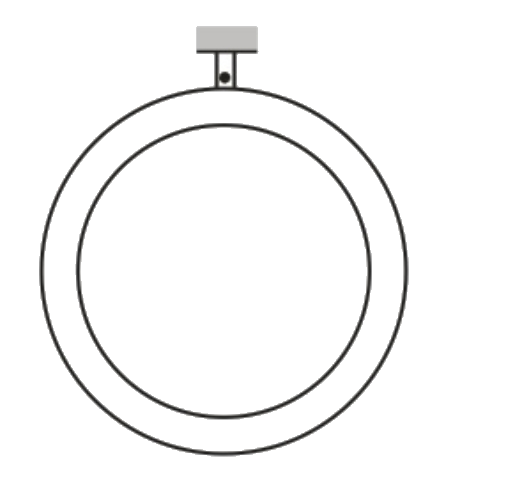
View SolutionA ring of radius R is suspended from its circumference and is made to oscillate about a horizontal axis in a vertical plane. The length equivalent to a simple pendulum will be :
View Solution

