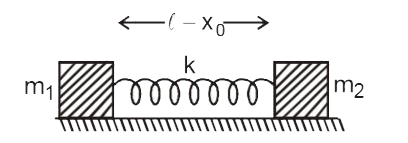
Two blocks of mass $m_{1}$ and $m_{2}$ are connected with a spring of natural length $l$ and spring constant k. The system is lying on a smooth horizontal surface. Initially spring is compressed by $x_{0}$ as shown in figure. Show that the two blocks will perform SHM about their equilibrium position. Also (a) find the time period, (b) find amplitude of each block and (c) length of spring as a function of time.

Video Solution

Text Solution

Verified by Experts

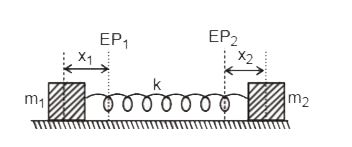
(a) Here both the blocks will be in equilibrium at the same time when spring is in its natural length. Let $E P_{1}$ and $E P_{2}$ be equilibrium positions of block A and B as shown in figure.
Let at any time during oscillations, blocks are at a distance of $x_{1}$ and $x_{2}$ from their equilibrium positions.
As no external force is acting on the spring block system
$∴ (m_{1} + m_{2}) Δ x_{cm} = m_{1} x_{1} - m_{2} n_{2} = 0$
or $m_{1} x_{1} = m_{2} x_{2}$
For 1st particle, force equation can be written as
$k (x_{1} + \frac{m_{1}}{m_{2}} x_{1}) = - m_{1} a_{1}$
or $a_{1} = - \frac{k (m_{1} + m_{2})}{m_{1} m_{2}} x_{1}$
$∴ ω_{1} = - \frac{k (m_{1} + m_{2})}{m_{1} m_{2}}$
Hence T = $2 π \sqrt{\frac{m_{1} m_{2}}{k (m_{1} + m_{2})}} = 2 π \sqrt{\frac{μ}{K}}$
were $μ = \frac{m_{1} m_{2}}{(m_{1} + m_{2})}$ which is know as reduced mass
(b) Let the amplitude of blocks be $A_{1}$ and $A_{2}$
$m_{1} A_{1} = m_{2} A_{2}$
By energy conservation ,
$\frac{1}{2} k {(A_{1} + A_{2})}_{1}^{2} = \frac{1}{2} k x_{0}^{2}$
or $A_{1} + A_{2} = x_{0}$
or $A_{1} + A_{2} = x_{0}$
or , $A_{1} + \frac{m_{1}}{m_{2}} A_{1} = x_{0}$
or $A_{1} = \frac{m_{2} x_{0}}{m_{1} + m_{2}}$
$A_{2} = \frac{m_{1} x_{0}}{m_{1} + m_{2}}$
(c) Let equilibrium position of 1st particle be origin, i.e., x = 0.
x co-ordinate of particles can be written as
$x_{1} = A_{1} cos ω t$ and $x_{2} = l - A_{2} cos ω t$
Hence, length of spring can be written as :
length $= x_{2} - x_{1}$
= $l - (A_{1} + A_{2}) cos ω t$

Updated on:21/07/2023

Class 12 PHYSICS SIMPLE HARONIC MOTION

Topper's Solved these Questions

Knowledge Check

Two blocks of masses $m_{1}$ and $m_{2}$ are connected by an ideal sprit, of force constant $k$ . The blocks are placed on smooth horizontal surface. A horizontal force $F$ acts on the block $m_{1}$ . Initially spring is relaxed, both the blocks are at rest.

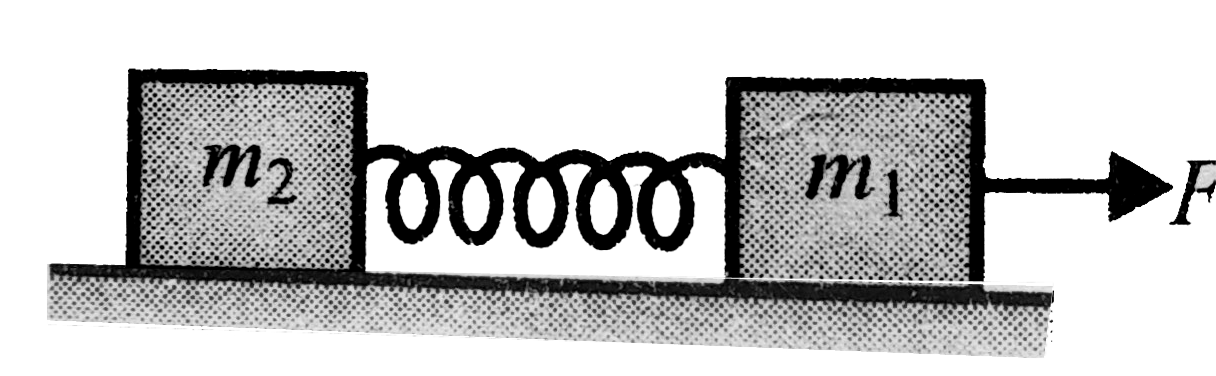
What is maximum elongation of spring.
A $\frac{2 m_{1} F}{(m_{1} + m_{2}) k}$
B $\frac{m_{1}^{2} F}{2 (m_{1} + m_{2}) k}$
C $\frac{2 m_{2} F}{k (m_{1} + m_{2})}$
D $\frac{m_{2}^{2} F}{2 {(m_{1} + m_{2})}_{1}^{2} k}$
Two blocks of masses $m_{1}$ and $m_{2}$ are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
Athe momentum of each particle remains constant separately
Bthe magnitude of momentums of each body are equal to each other
Cthe mechanical energy of system remains constant
Dboth (C) and (B) are correct
Two blocks A and B, each of mass m, are connected by a masslesss spring of natural length L and spring constant K. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B, and collides elastically with A. Then

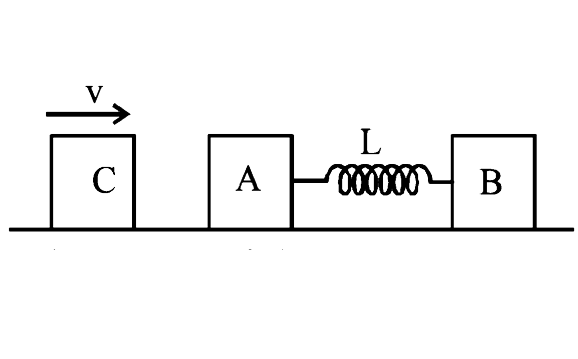Athe kinetic energy of the A-B system, at maximum compression of the spring, is zero.
Bthe kinetic energy of the A-B system, at maximum compression of the spring, is $m v^{2} / 4$ .
Cthe maximum compression of the spring is $v \sqrt{(m / K)}$
Dthe maximum compression of the spring is $v \sqrt{(m / 2 K)}$

MOTION-SIMPLE HARONIC MOTION -EXERCISE -4 (Leve-II) [ JEE 2011]

Home
Ask Doubt
Profile

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest. What is maximum elongation of spring.

Two blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :

MOTION-SIMPLE HARONIC MOTION -EXERCISE -4 (Leve-II) [ JEE 2011]

Two blocks of masses $m_{1}$ and $m_{2}$ are connected by an ideal sprit, of force constant $k$ . The blocks are placed on smooth horizontal surface. A horizontal force $F$ acts on the block $m_{1}$ . Initially spring is relaxed, both the blocks are at rest.

What is maximum elongation of spring.

Two blocks of masses $m_{1}$ and $m_{2}$ are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :