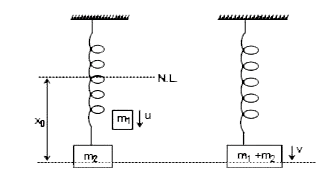
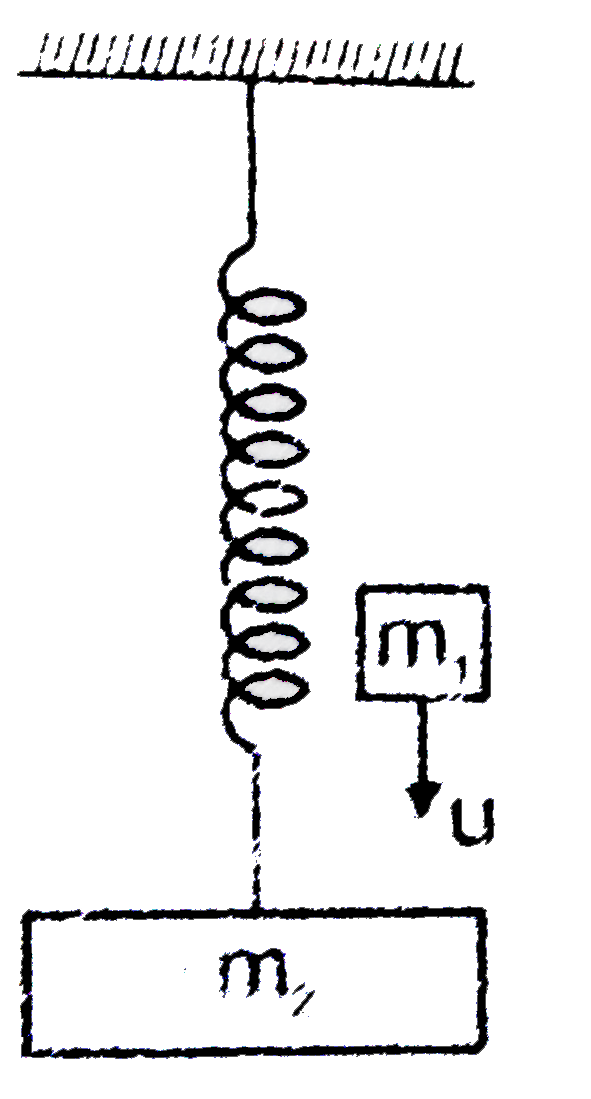
Block of mass m2 is in equilibrium and at rest. The mass m1 moving with velocity u vertically downwards collides with m2 and sticks to it. Find the energy of oscillation.
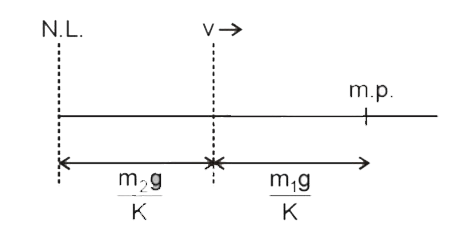
At equilibrium position m2g=kx0
⇒x0=m2gK
After collision m2 sticks to m1.
∴ By momentum conservation.
m1u=(m1+m2)v
v=m1um1+m2
Now both the blocks are executing S.H.M. which can be interpreted as follows:
Now , we know that v2=ω2(A2−x2) ⋯(1)
ω2=km1+m2
=>x=m1gk
Put the values of v, ω2 & x in eq. (1)
(m1um1+m2)2=(km1+m2)[A2−(m1gk)2]
⇒kA2=[(m21u2m1+m2)+(m1gk)2]
⇒ Energy of oscillation =12kA2
=12[(m21u2m1+m2)+(m21g2k)]
Topper's Solved these Questions
- SIMPLE HARONIC MOTION Book:MOTIONChapter:SIMPLE HARONIC MOTION Exercise:EXERCISE -1 ( SECTION-A )
Explore 8 Videos
- SIMPLE HARONIC MOTION Book:MOTIONChapter:SIMPLE HARONIC MOTION Exercise:EXERCISE -1 ( SECTION-B ) (Time per iod and angu larfrequency in SHM)
Explore 8 Videos
- SIMPLE HARMONIC MOTIONBook:MOTIONChapter:SIMPLE HARMONIC MOTIONExercise:EXERCISE -3 Section - B Previous Year Problems | JEE MAIN
Explore 23 Videos
- SOUND WAVESBook:MOTIONChapter:SOUND WAVESExercise:Exercise - 3 (Section - B)
Explore 14 Videos
Similar Questions
Block of mass m2 is in equilibrium and at rest. The mass m1 moving with velocity u vertically downwards collids with m2 and sticks to it. Find the energy of oscillation.
View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it. The speed of the system will be
View Solution
Knowledge Check
A particle of mass m moving with velocity v strikes a stationary particle of mass 2m and sticks to it. The speed of the system will be.
Av//2B2 vCv//3D3 vA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
A0.8vB0.2vC0.6vD0.4vTwo identical mass M moving with velocity u1andu2 collide perfectly inelastically. The loss in kinetic energy is
AM2(u2−u1)2BM2(u21−u22)CM4(u2−u1)2DM4(u21−u22)
An object of mass m1 moving with speed v collides with another object of mass m2 at rest and stick to it. Find the impulse imparted to the second object.
View SolutionBlock of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
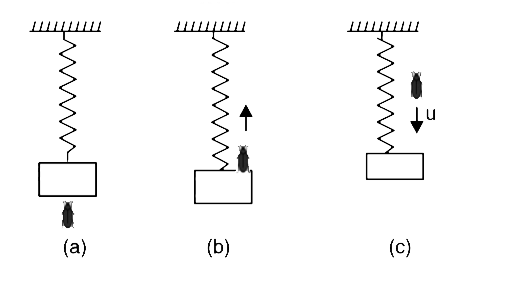
View SolutionA block of mass M is tied to a spring of force constant K and the system is suspended vertically. Consider three situations shown in fig. (a), (b) and (c).
(a) In fig. (a), an insect of mass M is clinging to the block and the system is in equilibrium. The insect leaves the block and falls. Find the amplitude of resulting oscillations.
(b) In fig. (b), an insect of mass M is resting on the top of the block and the system is in equilibrium. The insect suddenly jumps up with a speed u=g√MK and the block starts oscillating. Find amplitude of oscillation assuming that the insect never falls back on the block
(c) In fig. (c), an insect of mass M falls on the block this in equilibrium. The insect hits the block with velocity u=g√MK while moving downwards sticks to the block. Find the amplitude of oscillation.
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View Solution

