Center of mass of two thin uniform rods of same length but made up of different materials. & kept as shown, can be, if the meeting point is the origin of co-ordinated
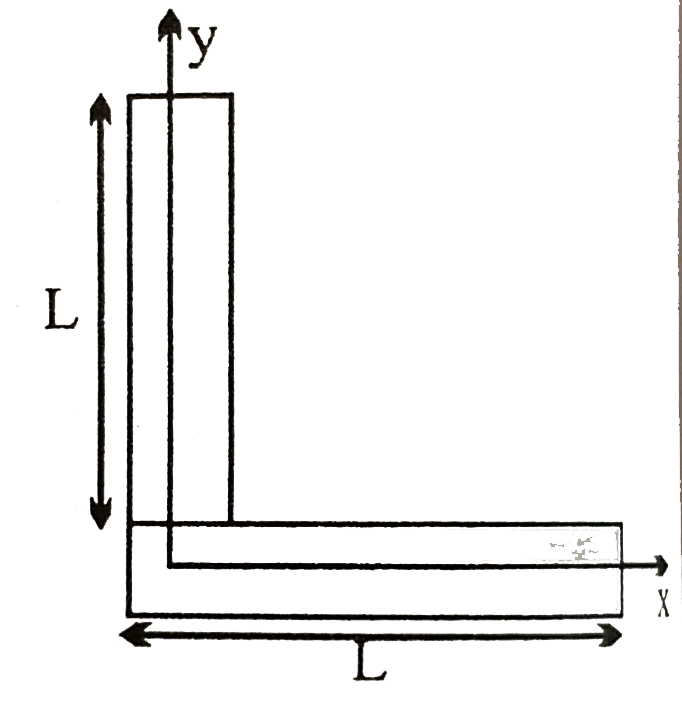
(L/2, L/2)
(2L/3, L/2)
(L/3, L/3)
(L/3, L/6)
The correct Answer is:D
Step by step video, text & image solution for Center of mass of two thin uniform rods of same length but made up of different materials. & kept as shown, can be, if the meeting point is the origin of co-ordinated by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 2 (Level-II)
28 Videos
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 3 Level-I
34 Videos
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 1
71 Videos
- Capacitance BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -4 LEVEL II
19 Videos
- CIRCULAR MOTIONBOOK - MOTIONCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE - 4
16 Videos
Similar Questions
Knowledge Check
Centre of mass of two unifrom rods of same length but made up of different materials & kept as shown, if the meeting point is the origin of co-ordinates :-
 A(L/2,L/2)B(2L/3,L/2)C(L/3,L/3)D(L/3,L/6)
A(L/2,L/2)B(2L/3,L/2)C(L/3,L/3)D(L/3,L/6)A convex lens is made up of three different materials as shown in the figure. For a point object placed on its axis, the number of images formed are
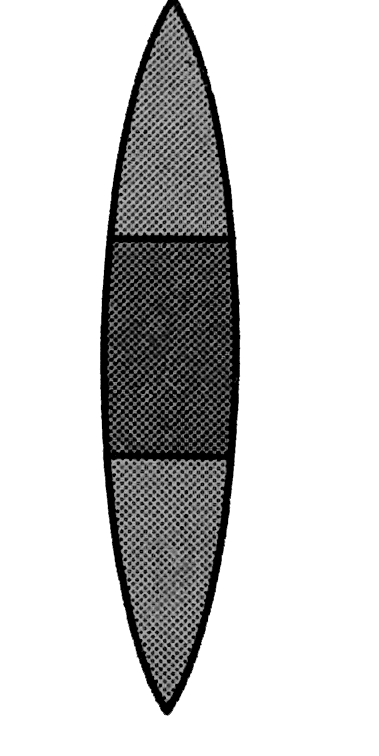 A1B5C4D3
A1B5C4D3A thin uniform rod of length L is bent at its mid point as shown in the figure. The distance of the centre of mass from the point O is
 AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2)
AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2)
Two spheres made of different materials but having the same mass, hace radii in the ratio of 3 : 4. Find the ratio of their densities.
View SolutionThree thin uniform rods made of same material are joined as shown. Locate x coordinate of COM.
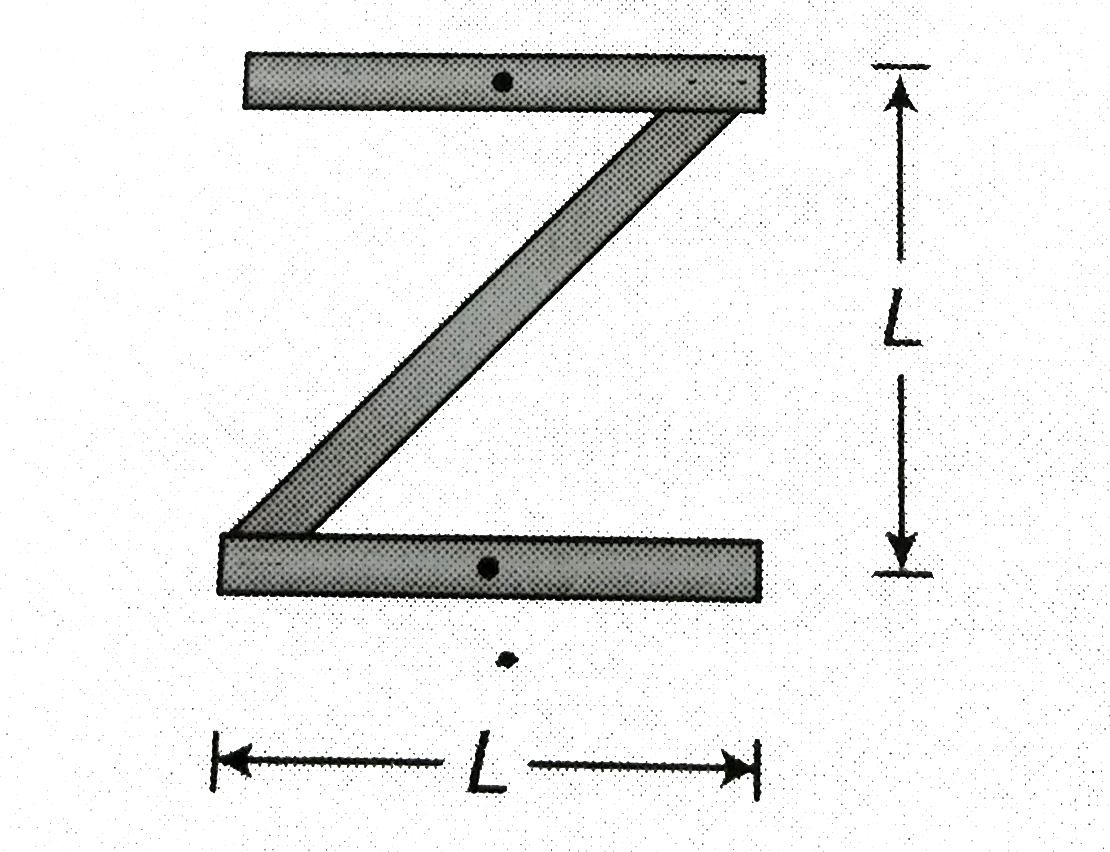
View SolutionIn a street light of mass M is suspended from the end of a uniform rod of length L in different possible patterns as shown in figure, then :
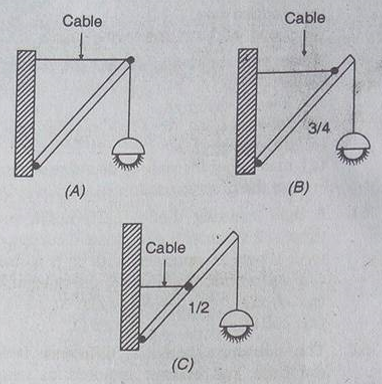
View SolutionIn a street light of mass M is suspended from the end of a uniform rod of length L in different possible patterns as shown in figure, then :

View SolutionThe moment of inertia of a thin uniform rod of mass M and length L about an axis perpendicular to the rod, through its centre is I. The moment of inertia of the rod about an axis perpendicular to rod through its end point is
View Solution

