A block is hanged from spring in a cage. Elongation in spring is ‘x1’ and ‘x2’ when cage moves up and down respectively with same acceleration. The expansion in spring when the cage move horizontally with same acceleration -
x1+x22
√x21−x222
√x21+x222
√x1x2
The correct Answer is:C
Step by step video, text & image solution for A block is hanged from spring in a cage. Elongation in spring is ‘x_(1)’ and ‘x_(2)’ when cage moves up and down respectively with same acceleration. The expansion in spring when the cage move horizontally with same acceleration - by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CENTRE OF MASSBook:MOTIONChapter:CENTRE OF MASSExercise:Exercise - 2 (Level-I)
Explore 40 Videos
- CENTRE OF MASSBook:MOTIONChapter:CENTRE OF MASSExercise:Exercise - 2 (Level-II)
Explore 28 Videos
- CENTRE OF MASSBook:MOTIONChapter:CENTRE OF MASSExercise:Exercise - 4 Level-II
Explore 20 Videos
- Capacitance Book:MOTIONChapter:Capacitance Exercise:EXERCISE -4 LEVEL II
Explore 19 Videos
- CIRCULAR MOTIONBook:MOTIONChapter:CIRCULAR MOTIONExercise:EXERCISE - 4
Explore 16 Videos
Similar Questions
A block is hanged from spring is a cage. Elogation is spring is x1=4√2nm and x2=3√2mm mm when cage moves up and down respectively with same acceleration. The expansion (in mm) in spring when the cage moves horizontally with the same acceleration .
View SolutionIf a monkey moves upward with respect to the rope with acceleration g/2 then acceleration of block, if masses of block and monkey are same
View Solution
Knowledge Check
A pendulum is hanging from the ceiling of a cage. If the cage moves up with constant acceleration a, its tension is T1 and if it moves down with same acceleration, the corresponding tension is T2. The tension in the string if the cage moves horizontally with same acceleration a is
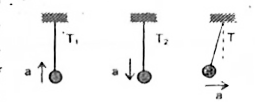 A√T21+T222B⎛⎜ ⎜⎝√T21−T222⎞⎟ ⎟⎠C⎛⎜ ⎜⎝√T21+T222⎞⎟ ⎟⎠Dnone of the above.
A√T21+T222B⎛⎜ ⎜⎝√T21−T222⎞⎟ ⎟⎠C⎛⎜ ⎜⎝√T21+T222⎞⎟ ⎟⎠Dnone of the above.A pendulum is hanging from the ceiling of a cage . If the cage moves up with constant accelration 'a' the tension is T1. If it moves down with the same acceleration 'a' then tension is T2. If the cage moves horizontally with the same accelration 'a', then the tension is T in equilibrium w.r.t. cage. Then 2T−2 is
AT21+T22B(T1+T2)2C2T1T2D4T1T2A pendulum bob is hanging from the roof of an elevator with the help of a light string. When the elevator moves up with uniform acceleration 'a' the tension in the string is T1. When the elevator moves down with the same acceleration, the tension in the string is T2. If the elevator were stationary, the tension in the string would be
AT1+T22B√T1+T2CT1T2T1+T2D2T1T2T1+T2
A small metal sphere is suspended from a light spring of force constant k from the ceiling of a cage.The cage is uniformly accelerated upward by a force F.If the cage is n times heavier than the sphere the potential energy stored in the spring when the sphere has the same acceleration as that of the cage is
View SolutionA pendulum bob is hanging from the roof of an elevator with the help of a light string. When the elevator moves up with uniform acceleration 'a' the tension in the string is T1.When the elevator moves down with the same acceleration, the tension in the string is T1 .If the elevator were stationary, the tension in the string would be
View SolutionBlock A of mass m is placed on a plank B . A light support S is fixed on plank B and is attached with the block A with a spring of spring constant K. Consider that initialy spring is in the natural length, and the system is at rest. Find the maximum compression in the spring, if the plank B is moved with a constant acceleration 'a' . (All the surface are smooth) :
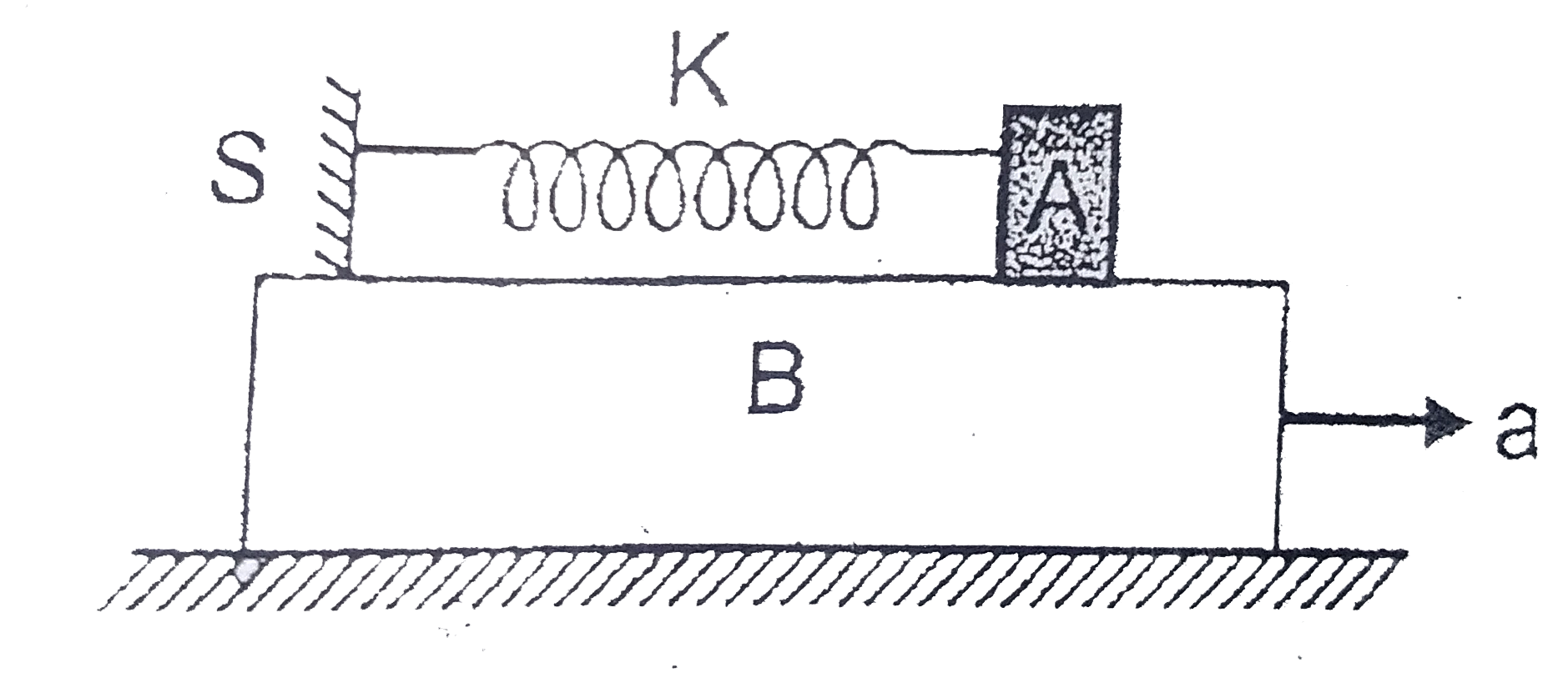
View SolutionA block ofmass m is attached with a spring in its natural length, of spring constant k. The other end A of spring is moved with a constant acceleration 'a' away from the block as shown in the figure−3.74. Find the maximum extension in the spring. Assume that initially block and spring is at rest w.r.t ground frame:

View SolutionA block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be

View Solution

