A block is hanged from spring is a cage. Elogation is spring is x1=4√2nm and x2=3√2mm mm when cage moves up and down respectively with same acceleration. The expansion (in mm) in spring when the cage moves horizontally with the same acceleration .
The correct Answer is:5
To solve the problem step by step, we will analyze the situation of the block hanging from the spring in the cage and how the elongation of the spring changes with different movements of the cage.
1. Understanding the Problem:
- A block is hanging from a spring in a cage.
- The elongation of the spring when the cage moves up with acceleration a is given as x1=4√2nm.
- The elongation of the spring when the cage moves down with the same acceleration is x2=3√2mm.
- We need to find the elongation of the spring when the cage moves horizontally with the same acceleration.
2. Effective Acceleration:
- When the cage moves upward, the effective acceleration acting on the block is g+a.
- When the cage moves downward, the effective acceleration is g−a.
3. Using Hooke's Law:
- According to Hooke's law, the force exerted by the spring is proportional to its elongation:
F=kx
- Where k is the spring constant and x is the elongation.
4. Setting Up the Equations:
- For upward motion:
kx1=m(g+a)(1)
- For downward motion:
kx2=m(g−a)(2)
5. Substituting the Given Values:
- From equation (1):
k(4√2nm)=m(g+a)
- From equation (2):
k(3√2mm)=m(g−a)
6. Equating the Two Expressions:
- Rearranging both equations gives:
g+a4√2=g−a3√2
- Cross-multiplying yields:
3√2(g+a)=4√2(g−a)
- Simplifying this gives:
3g+3a=4g−4a
- Rearranging terms:
7a=g⇒a=g7(3)
7. Finding the Elongation for Horizontal Motion:
- When the cage moves horizontally with acceleration a, the effective acceleration is:
geff=√a2+g2
- Substituting a from equation (3):
geff=√(g7)2+g2=√g249+g2
- Combining the terms:
geff=√g2+49g249=√50g249=g√507
8. Using Hooke's Law Again:
- The elongation x for horizontal motion is given by:
kx=mgeff⇒x=mgeffk
- Substituting geff:
x=m⋅g√507k
9. Relating to Previous Cases:
- From previous elongation equations, we can find the relationship and solve for x:
x=5mm
Final Answer:
The expansion in the spring when the cage moves horizontally with the same acceleration is x=5mm.
- A block is hanging from a spring in a cage.
- The elongation of the spring when the cage moves up with acceleration a is given as x1=4√2nm.
- The elongation of the spring when the cage moves down with the same acceleration is x2=3√2mm.
- We need to find the elongation of the spring when the cage moves horizontally with the same acceleration.
- When the cage moves upward, the effective acceleration acting on the block is g+a.
- When the cage moves downward, the effective acceleration is g−a.
- According to Hooke's law, the force exerted by the spring is proportional to its elongation:
F=kx
- Where k is the spring constant and x is the elongation.
- For upward motion:
kx1=m(g+a)(1)
- For downward motion:
kx2=m(g−a)(2)
- From equation (1):
k(4√2nm)=m(g+a)
- From equation (2):
k(3√2mm)=m(g−a)
- Rearranging both equations gives:
g+a4√2=g−a3√2
- Cross-multiplying yields:
3√2(g+a)=4√2(g−a)
- Simplifying this gives:
3g+3a=4g−4a
- Rearranging terms:
7a=g⇒a=g7(3)
- When the cage moves horizontally with acceleration a, the effective acceleration is:
geff=√a2+g2
- Substituting a from equation (3):
geff=√(g7)2+g2=√g249+g2
- Combining the terms:
geff=√g2+49g249=√50g249=g√507
- The elongation x for horizontal motion is given by:
kx=mgeff⇒x=mgeffk
- Substituting geff:
x=m⋅g√507k
- From previous elongation equations, we can find the relationship and solve for x:
x=5mm
The expansion in the spring when the cage moves horizontally with the same acceleration is x=5mm.
Topper's Solved these Questions
Similar Questions
If a monkey moves upward with respect to the rope with acceleration g/2 then acceleration of block, if masses of block and monkey are same
View SolutionA balloon of mass m is descending down with an acceleration How much mass should be g2 removed from it so that it starts moving up with same acceleration?
View Solution
Knowledge Check
A block is hanged from spring in a cage. Elongation in spring is ‘x1’ and ‘x2’ when cage moves up and down respectively with same acceleration. The expansion in spring when the cage move horizontally with same acceleration -
Ax1+x22B√x21−x222C√x21+x222D√x1x2A pendulum is hanging from the ceiling of a cage. If the cage moves up with constant acceleration a, its tension is T1 and if it moves down with same acceleration, the corresponding tension is T2. The tension in the string if the cage moves horizontally with same acceleration a is
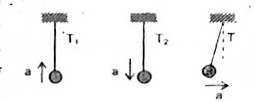 A√T21+T222B⎛⎜ ⎜⎝√T21−T222⎞⎟ ⎟⎠C⎛⎜ ⎜⎝√T21+T222⎞⎟ ⎟⎠Dnone of the above.
A√T21+T222B⎛⎜ ⎜⎝√T21−T222⎞⎟ ⎟⎠C⎛⎜ ⎜⎝√T21+T222⎞⎟ ⎟⎠Dnone of the above.A pendulum is hanging from the ceiling of a cage . If the cage moves up with constant accelration 'a' the tension is T1. If it moves down with the same acceleration 'a' then tension is T2. If the cage moves horizontally with the same accelration 'a', then the tension is T in equilibrium w.r.t. cage. Then 2T−2 is
AT21+T22B(T1+T2)2C2T1T2D4T1T2
A balloon of mass m is descending down with an g/2 acceleration How much mass should be removed from it so that it starts moving up with same acceleration
View SolutionThe apparent weight of a man in a lift is W1 when lift moves upwards with some acceleration and is W2 when it is accerating down with same acceleration. Find the true weight of the man and acceleration of lift .
View SolutionA small metal sphere is suspended from a light spring of force constant k from the ceiling of a cage.The cage is uniformly accelerated upward by a force F.If the cage is n times heavier than the sphere the potential energy stored in the spring when the sphere has the same acceleration as that of the cage is
View SolutionA pendulum bob is hanging from the roof of an elevator with the help of a light string. When the elevator moves up with uniform acceleration 'a' the tension in the string is T1. When the elevator moves down with the same acceleration, the tension in the string is T2. If the elevator were stationary, the tension in the string would be
View SolutionA pendulum bob is hanging from the roof of an elevator with the help of a light string. When the elevator moves up with uniform acceleration 'a' the tension in the string is T1.When the elevator moves down with the same acceleration, the tension in the string is T1 .If the elevator were stationary, the tension in the string would be
View Solution