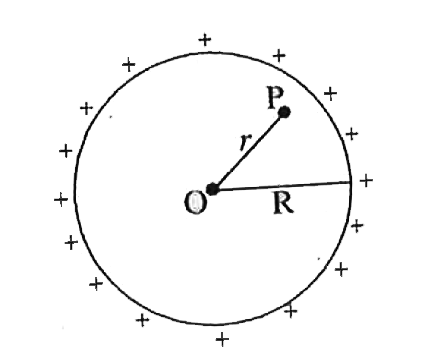
सिद्ध कीजिए कि आवेशित गोलीय कोश के अंदर विभव का मान उतना ही है जितना पृष्ठ पर|
दो भागों में विभक्त कर हल करते हैं-
(1 ) अनन्त से दुरी R तक तथा
(2 ) दुरी R से अभीष्ट बिन्दु की दुरी r तक अर्थात
समीकरण (1 ) से स्पष्ट है कि गोलीय कोश के आन्तरिक बिन्दु पर विद्युत विभव का मान पृष्ठ पर स्थित बिन्दु के विधुत विभव के मान के बराबर होता है |
अर्थात
Topper's Solved these Questions
- विद्युत विभव Book:SANJEEV PUBLICATIONChapter:विद्युत विभव Exercise:अभ्यास (पाठ्यपुस्तक के प्रश्न) (निबन्धात्मक प्रश्न - )
Explore 5 Videos
- विद्युत विभव Book:SANJEEV PUBLICATIONChapter:विद्युत विभव Exercise:अभ्यास (पाठ्यपुस्तक के प्रश्न) (आंकिक प्रश्न - )
Explore 22 Videos
- विद्युत विभव Book:SANJEEV PUBLICATIONChapter:विद्युत विभव Exercise:अभ्यास (पाठ्यपुस्तक के प्रश्न) (अतिलघुउत्तरीय प्रश्न -)
Explore 20 Videos
- विद्युत परिपथ Book:SANJEEV PUBLICATIONChapter:विद्युत परिपथ Exercise:उच्चस्तरीय बुद्धि -कौशल प्रश्न
Explore 5 Videos
- विधुत क्षेत्र Book:SANJEEV PUBLICATIONChapter:विधुत क्षेत्र Exercise:अन्य महत्तवपूर्ण प्रश्न
Explore 54 Videos
Similar Questions
किसी बिंदु आवेश के कारण किसी बिंदु पर विद्युत् विभव का व्यंजक व्युत्पन्न कीजिए |
View Solutionदो बिंदुओं के मध्य 3 C आवेश को ले जाने में 6 जूल कार्य करना पड़ता है | इन बिंदुओं के मध्य विद्युत् विभवांतर ज्ञात कीजिए |
View Solutionविद्युत विभव अदिश राशि है अथवा सदिश राशि, बताइए |
View Solutionएक विभवमापी के प्राथमिक परिपथ में 0.2A धारा है। विभवमापी के तार का विशिष्ट प्रतिरोध ओर परिच्छेद क्षेत्रफल क्रमशः 4×10−7Ω−m और 8×10−7m2 है। विभव प्रवणता का मान ज्ञात कीजिए।
View Solutionकिसी विद्युत द्विध्रुव के निरक्षीय रेखा पर स्थित बिंदु पर विद्युत क्षेत्र की दिशा क्या होती है?
View Solutionकिसी बिंदु आवेश के कारण उस बिंदु को केंद्र मानकर खींचे गए 10cm त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स −1.0×103Nm2/C त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स। (a) यदि गॉऊसीय पृष्ठ की त्रिज्या दो गुनी कर दी जाए तो पृष्ठ से कितना फ्लक्स गुजरेंगा ? (b) बिंदु आवेश का मान क्या है।
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionसिद्ध कीजिए कि किसी गुणोत्तर श्रेढ़ी के आरम्भ और अंत से संदुररस्थ पदों का गुणनफलन सदैव अचर रहता है ।
View Solutionएक अनन्त गुणोत्तर श्रेढी का योग x है तथा श्रेढी के सभी पदों का वर्ग करने पर श्रेढी का योग y है । सिद्ध कीजिए कि श्रेढी का सार्व अनुपात x2−yx2+y है ।
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि फलन f(x)=|x|,x=0 पर अवकलनीय नहीं है यद्यपि यह x=0 पर संतत है|
View Solutionसिद्ध कीजिए कि एक पासो के जोड़े को फेंकने पर पहले पर 5 आना , दूसरे पास पर 6 आने कि स्वतन्त्र घटनाएँ है।
View Solutionछाया मत छूना' कविता में 'जितना ही दौड़ा तू उतना ही भरमाया' के माध्यम से कवि क्या कहना चाहता है?
View Solutionअथवा 'कारतूस' पाठ के आधार पर सोदाहरण सिद्ध कीजिए कि वज़ीर अली एक जांबाज़ सिपाही था।
View Solutionगोलीय पृष्ठ पर अपवर्तन
View SolutionRecap|एक समान आवेशित खोखले गोलीय चालक के कारण विभव |OMR|Summary
View Solution