A ball is dropped from a height of a height of 90 m on a floor. At each collision with the floor, the ball loses one-tenth of its speed. Plot the speed -time graph of its motion between t = 0 to 12 s.
Ball is dropped from a height, s = 90 m
Initial velocity of the ball, u = 0
Acceleration, a = g = 9.8m/s2
Final velocity of the ball = v
From second equation of motion, time (t) taken by the ball to hit the ground can be obtained as:
s=ut+12at2
90=0+12×9.8t2
t=√18.38=4.29s
From first equation of motion, final velocity is given as:
v = u + at
= 0 + 9.8 × 4.29 = 42.04 m/s
Rebound velocity of the ball, ur=910v=910×42.04=37.84m/s
Time (t) taken by the ball to reach maximum height is obtained with the help of first equation of motion as:
v=ur+at'
0 = 37.84 + (– 9.8) t′
t'=−37.84−9.8=3.86s
Total time taken by the ball = t + t′ = 4.29 + 3.86 = 8.15 s
As the time of ascent is equal to the time of descent, the ball takes 3.86 s to strike back on the floor for the second time.
The velocity with which the ball rebounds from the floor =910×37.84=34.05 m/s
Total time taken by the ball for second rebound = 8.15 + 3.86 = 12.01 s
The speed-time graph of the ball is represented in the given figure as:
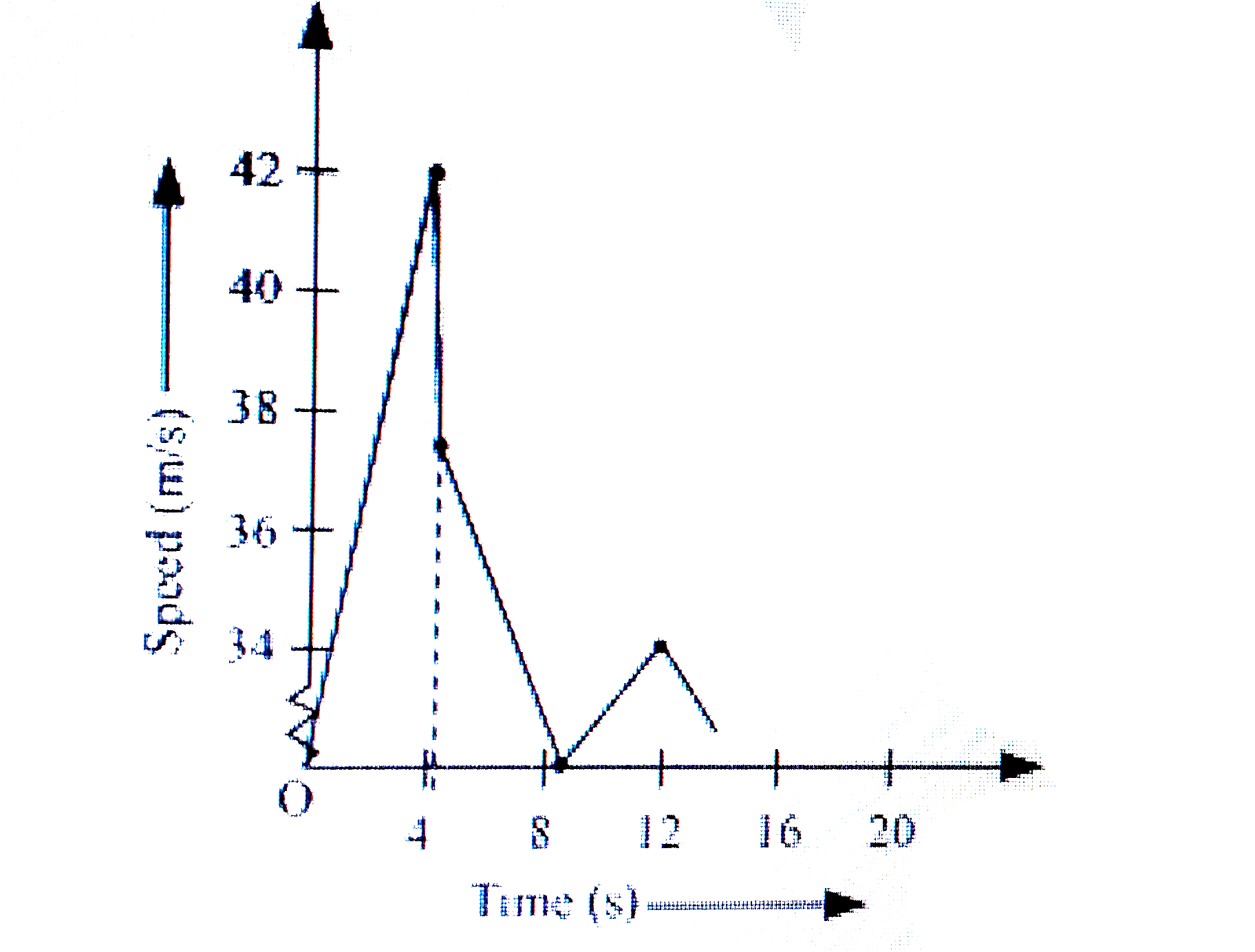
Topper's Solved these Questions
Similar Questions
A ball is dropped from a height of a height of 90 m on a floor. At each collsion with the floor , the ball loses one - tenth of its speed . Plot the speed -time graph of its motion between t 0 to 12 s.
View SolutionA ball is dropped from a height of 80 m on a floor. At each collision, the ball loses half of its speed. Plot the speed-time graph and velocity-time graph of its motion till two collisions With the floor. [Take g=10m/s2]
View Solution
Knowledge Check
A ball is dropped from a height of 20m on a floor for which e=1/2. The height attained by the ball after the second collision
A1.25mB2.5mC5mD10mA ball is dropped from a certain height on a horizontal floor. The coefficient of restitution between the ball and the floor is 12. The displacement time graph of the ball will be.
A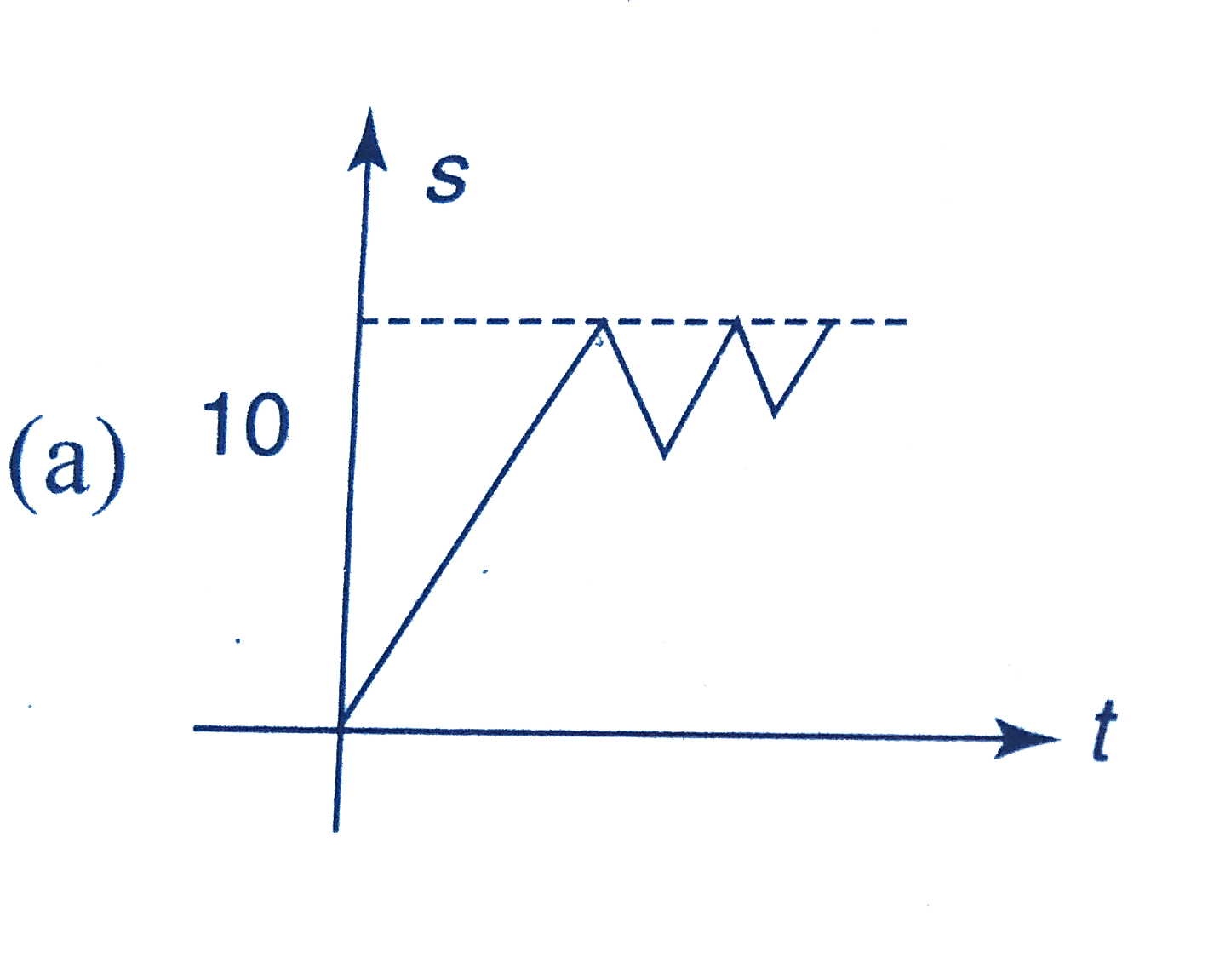 .B
.B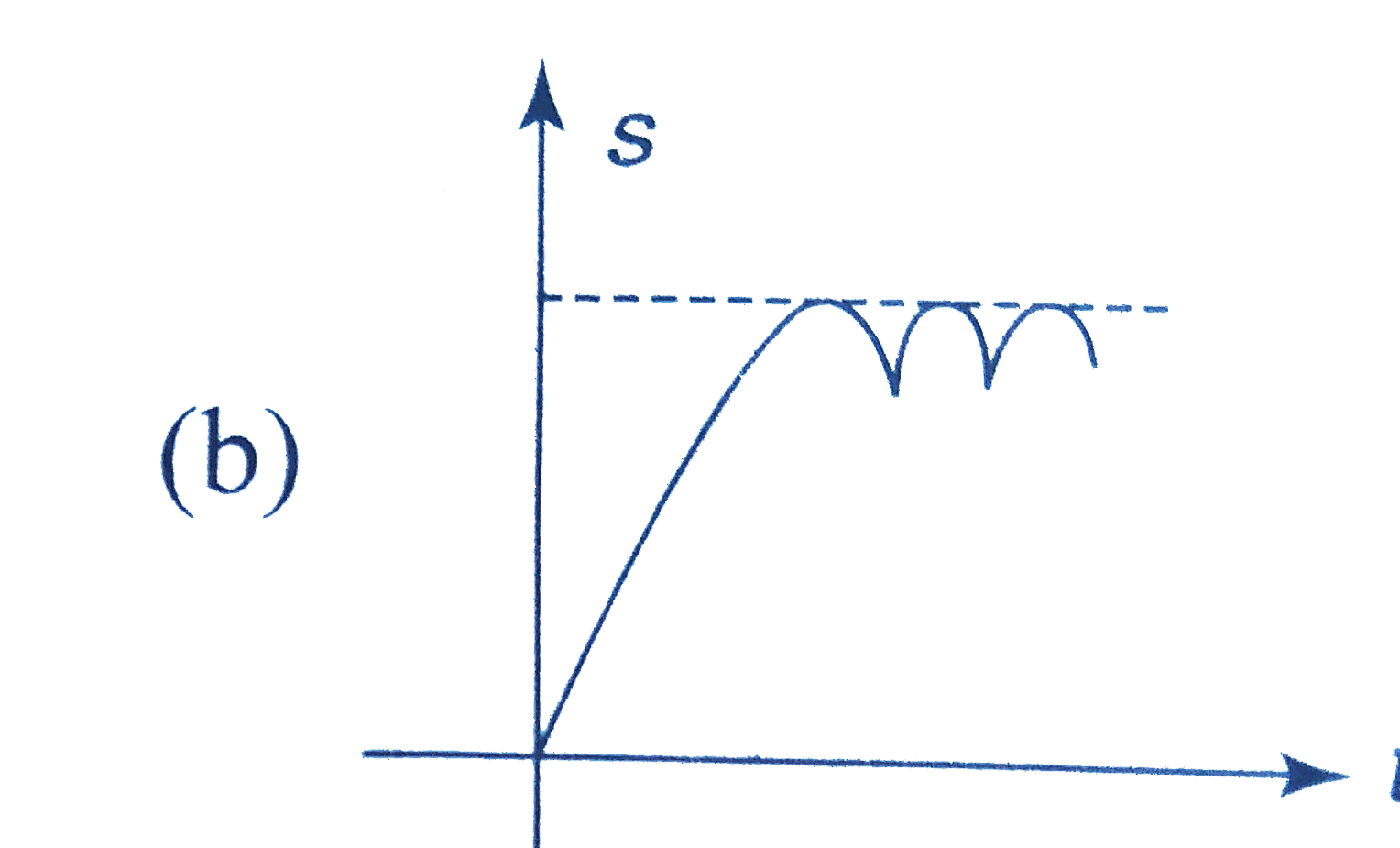 .C
.C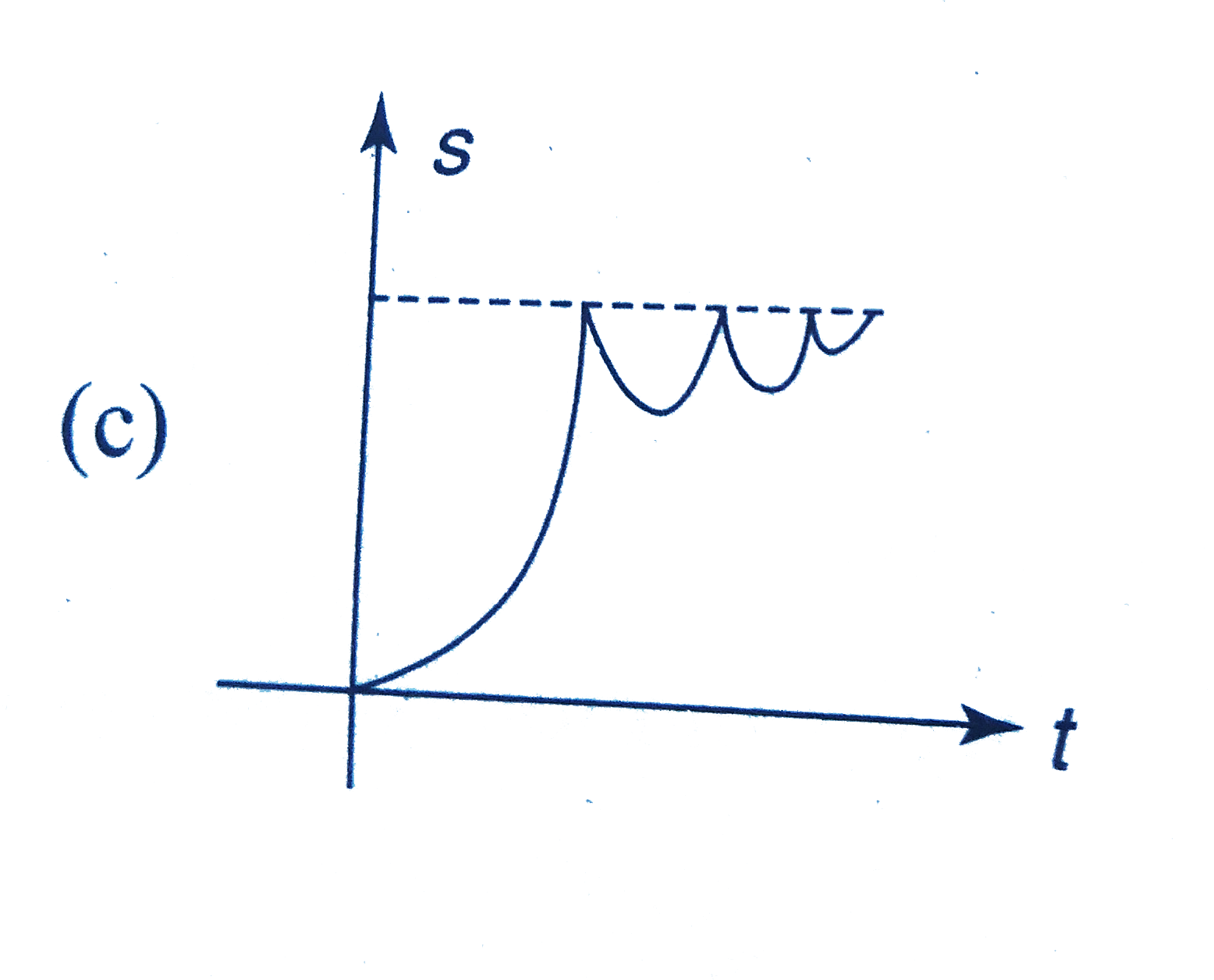 .D
.D .
.If a ball is dropped from height 2 metre on a smooth eleastic floor, then the time period of oscillation is
A2gB2√gC4gD4√g
A ball is dropped from a height h on to a floor . If the cofficient of restitution is e, calculate the height the ball first rebounds ?
View SolutionA ball is dropped from a height of 20 m in the floor and rebounds to 1.25 m after second collision, then coefficient of restitution e is
View SolutionA ball is dropped from a height of 20 m in the floor and rebounds to 1.25 m after second collision, then coefficient of restitution e is
View SolutionA ball of mass 1 kg is dropped from a height of 5 m. What is its speed at this instant ?
View SolutionA ball is dropped from a height h on to a floor. If in each collision its speed becomes e times of its striking value (a) find the time taken by ball to stop rebounding (b) find the total change in momentum in this time (c) find the average force exerted by the ball on the floor using results of part (a) and (b).
View Solution

