Let us consider an equaiton
12mv2=mgh,
Where m is the mass of the body, υ its velocity, g is acceleration due to gravity and h is the height. Cheak whether this equation is dimensionally correct.
The dimensions of LHS are
[M][LT−1]2=[M][L2T−2]
=[ML2T−2]
the dimensions of RHS are
[M][LT−2][L]=[M][L2T−2]
=[ML2T−2]
The dimensions of LHS and RHS are the same and hence the equation is dimensionally correct.
Topper's Solved these Questions
- UNITS AND MEASUREMENTBOOK - NCERTCHAPTER - UNITS AND MEASUREMENTEXERCISE - EXERCISE
33 Videos
- UNITS AND MEASUREMENTBOOK - NCERTCHAPTER - UNITS AND MEASUREMENTEXERCISE - QUESTION
1 Video
- THERMODYNAMICSBOOK - NCERTCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE
10 Videos
- WAVESBOOK - NCERTCHAPTER - WAVESEXERCISE - EXERCISE
27 Videos
Similar Questions
Let us consider an equation
12με2=mgh,
Where m is the mass of the body, υ its velocity, g is acceleration due to gravity and h is the height. Check whether this equation is dimensionally correct.
View SolutionTaking the value of the acceleration due toj gravity as 10 m s^(-2) , Find its value in km h^(-2).
View Solution
Knowledge Check
Find ratio of acceleration due to gravity g at depth d and at height h where d=2h
A1:1B1:2C2:1D1:4The velocity of a freely falling body changes as gphqwhere g is acceleration due to gravity and h is the height. The values of p and q are
A1,12B12,12C12,1D1,1The displacement of a body is given by s=12gt2 where g is acceleration due to gravity. The velocity of the body at any time t is
Agt36Bgt22CgtDgt2
Show dimensionally that the relation t=2π(Ig)
is incorrect, where I is length and t is time period of a simple pendulum , g is acc. Due to gravity. Find the correct form of the relation, dimensionally
View SolutionThe terminal velocity v of a small steel ball ofradius r fal ling under gravity through a column ofa viscous liquid of coefficient of viscosity η depends on mass of the ball m, acceleration due to gravity g, coefficient of viscosity η and radius r. Which of the following relations is dimensionally correct?
View SolutionThe Bernoulli's equation is given by P+12ρv2+hρg=k. Where P= pressure, ρ= density, v= speed, h=height of the liquid column, g= acceleration due to gravity and k is constant. The dimensional formula for k is same as that for:
View SolutionA ball is thrown upwards . Its height varies with time as shown in figure. If the acceleration due to gravity is 7.5m/s2, then the height h is
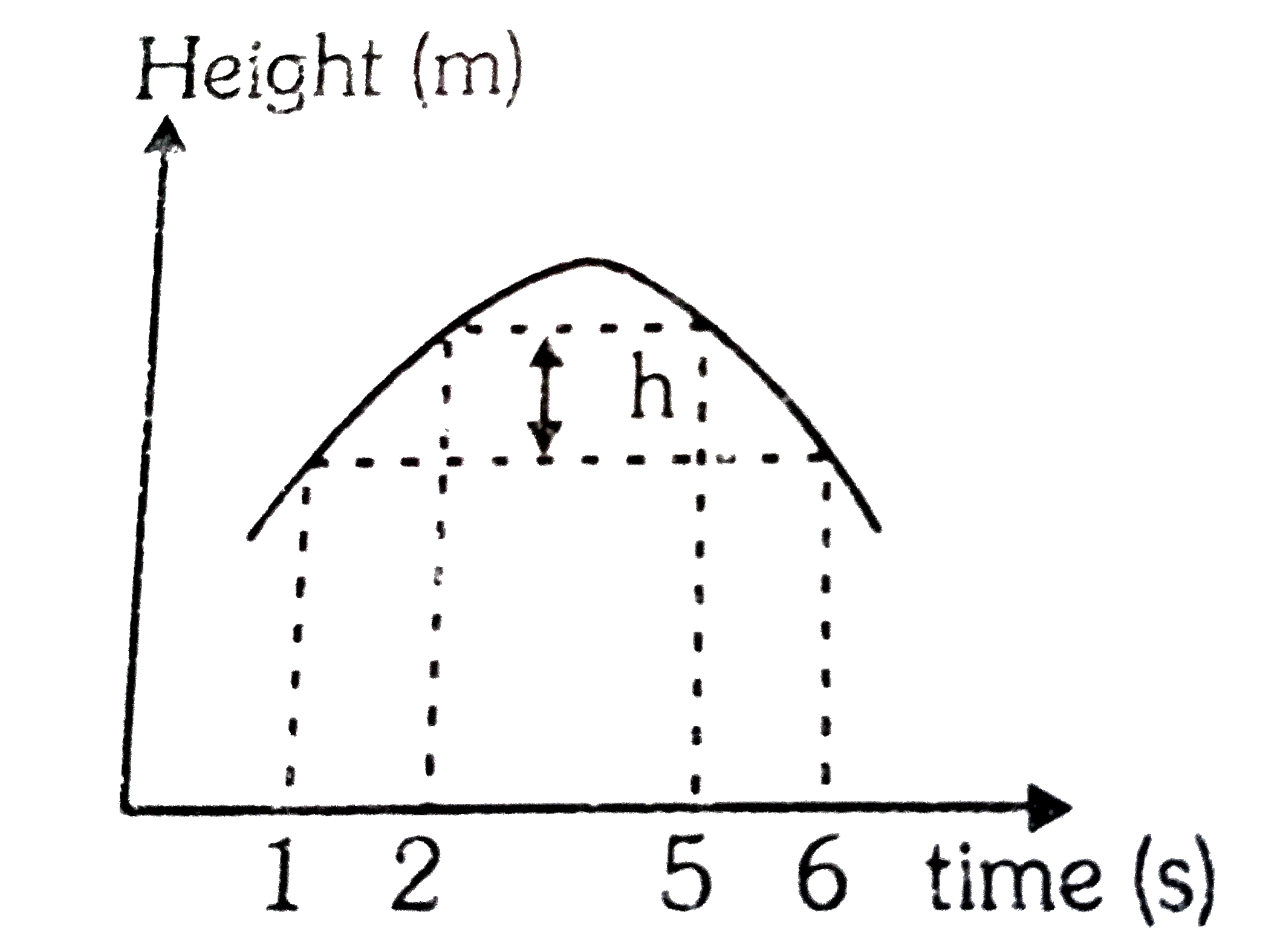
View SolutionAn earth satellite of mass m revolves in a circular orbit at a height h from the surface of the earth. R is the radius of the earth and g is acceleration due to gravity at the surface of the earth. The velocity of the satellite in the orbit is given by
View Solution