Let us consider an equation
12με2=mgh,
Where m is the mass of the body, υ its velocity, g is acceleration due to gravity and h is the height. Check whether this equation is dimensionally correct.
L.H.S.=12mυ2=M(LT−1)2
=[M1L2T−2]
R.H.S.=mgh=M(LT−2)(L)=[M1L2T−2]
As L.H.S. = R.H.s., dimensionally,
The equation is dimensionally correct.
Topper's Solved these Questions
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Conceptual Problem
Explore 65 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:NCERT Exercises
Explore 40 Videos
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:multiple choice Questions
Explore 13 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions
Explore 7 Videos
Similar Questions
Show dimensionally that the relation t=2π(Ig)
is incorrect, where I is length and t is time period of a simple pendulum , g is acc. Due to gravity. Find the correct form of the relation, dimensionally
View SolutionPotential energy of a body depends on :
(i) Mass of the body (m) .
(ii) Acceleration due to gravity (g) .
(iii) Height of the body with respect to ground (h).
View Solution
Knowledge Check
Find ratio of acceleration due to gravity g at depth d and at height h where d=2h
A1:1B1:2C2:1D1:4The velocity of a freely falling body changes as gphqwhere g is acceleration due to gravity and h is the height. The values of p and q are
A1,12B12,12C12,1D1,1The displacement of a body is given by s=12gt2 where g is acceleration due to gravity. The velocity of the body at any time t is
Agt36Bgt22CgtDgt2
Taking the value of the acceleration due toj gravity as 10 m s^(-2) , Find its value in km h^(-2).
View SolutionFind the dimensions of K in the relation T=2π√KI2gmG where T is time period, I is length, m is mass, g is acceleration due to gravity and G is gravitational constant.
View SolutionAssertion : In the equation, s=u+at−12a where, s is the distance travelled by uniformly accelerated body in tth second.
Reason : The above equation is dimensionally incorrect.
View SolutionA ball is thrown upwards . Its height varies with time as shown in figure. If the acceleration due to gravity is 7.5m/s2, then the height h is
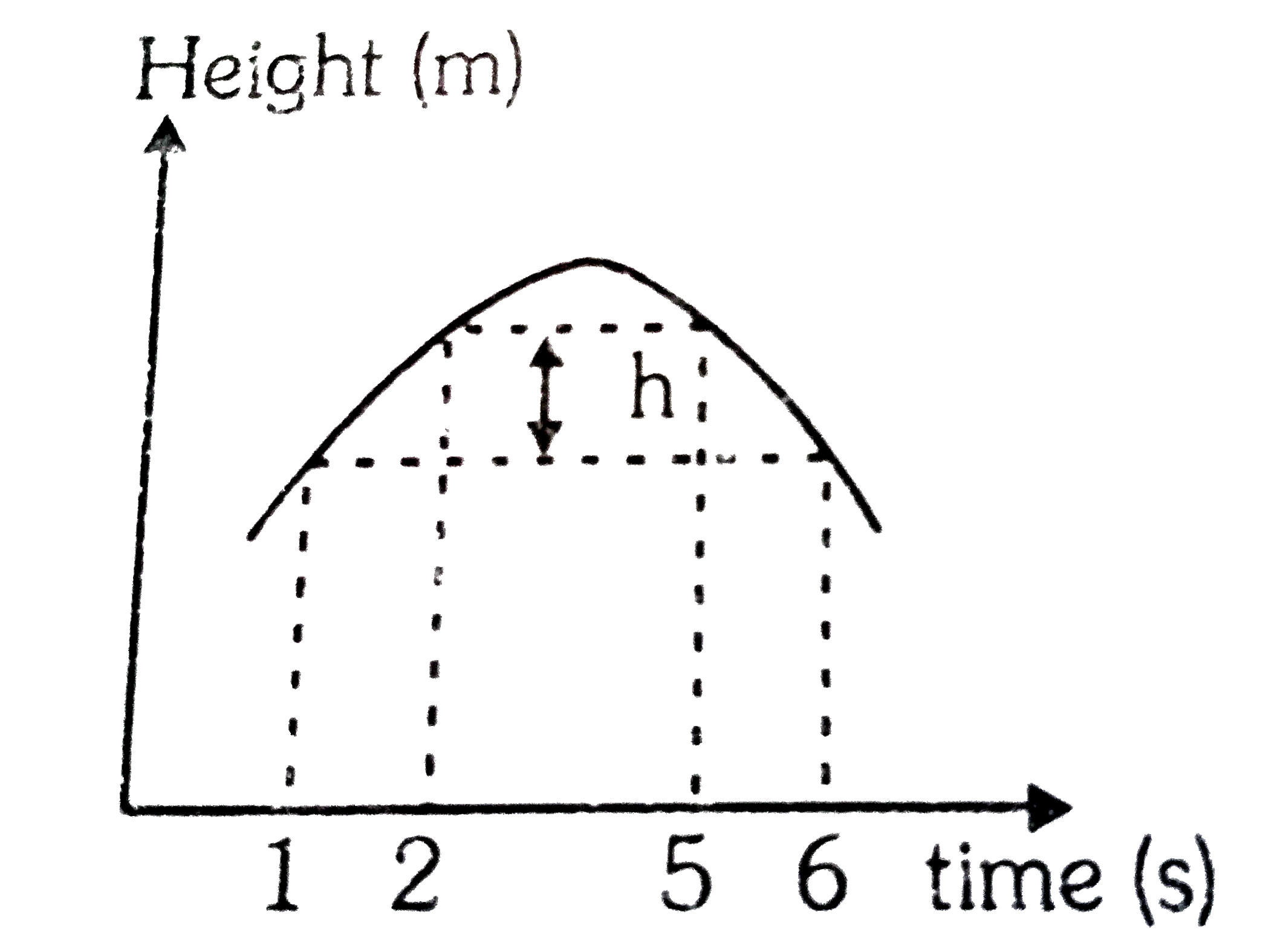
View SolutionThe Bernoulli's equation is given by P+12ρv2+hρg=k. Where P= pressure, ρ= density, v= speed, h=height of the liquid column, g= acceleration due to gravity and k is constant. The dimensional formula for k is same as that for:
View Solution