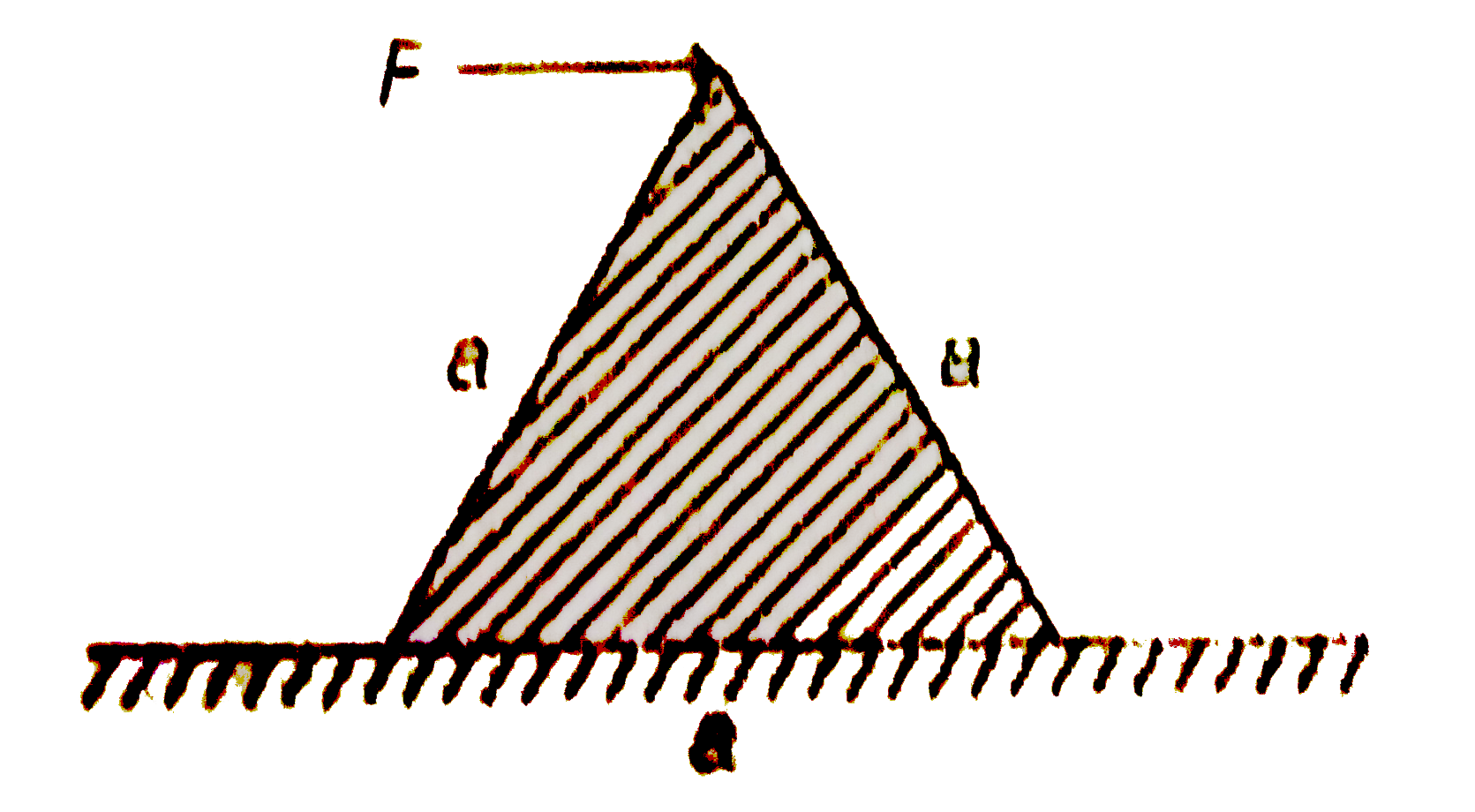
A horizontal force F is applied at the top of an equilateral triangular block having mass m. The minimum coefficient of friction required to topple the block before translation is μ find 100μ? (√3=1.74)
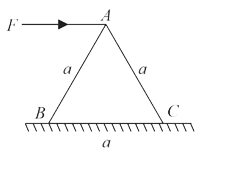
The correct Answer is:58
For toppling
F.a√32=mga2,F=mg√3
For not sliding F<μmg,mg√3≤μmg
μ≥1√3
Similar Questions
A cubical box of side length L rests on a rough horizontal surface having coefficient of friction μ. A variable horizontal force F=αt is applied on the top of the block as shown in figure, where α is a constant and t is time. The coefficient of friction is sufficient so that the block does not slide before toppling. The graph between torque due to normal reaction about end B and time before toppling start is

View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction μ . A horizontal force F is applied on the top of prism as shown in figure. If the coefficient of friction is sufficiently high so that the prism does not slide before topping, the minimum force required to topple the prism is

View Solution
Knowledge Check
A horizontal force F is applied at the top of an equilateral triangular block having mass m. The minimum coefficient of friction required to topple the block before translation will be
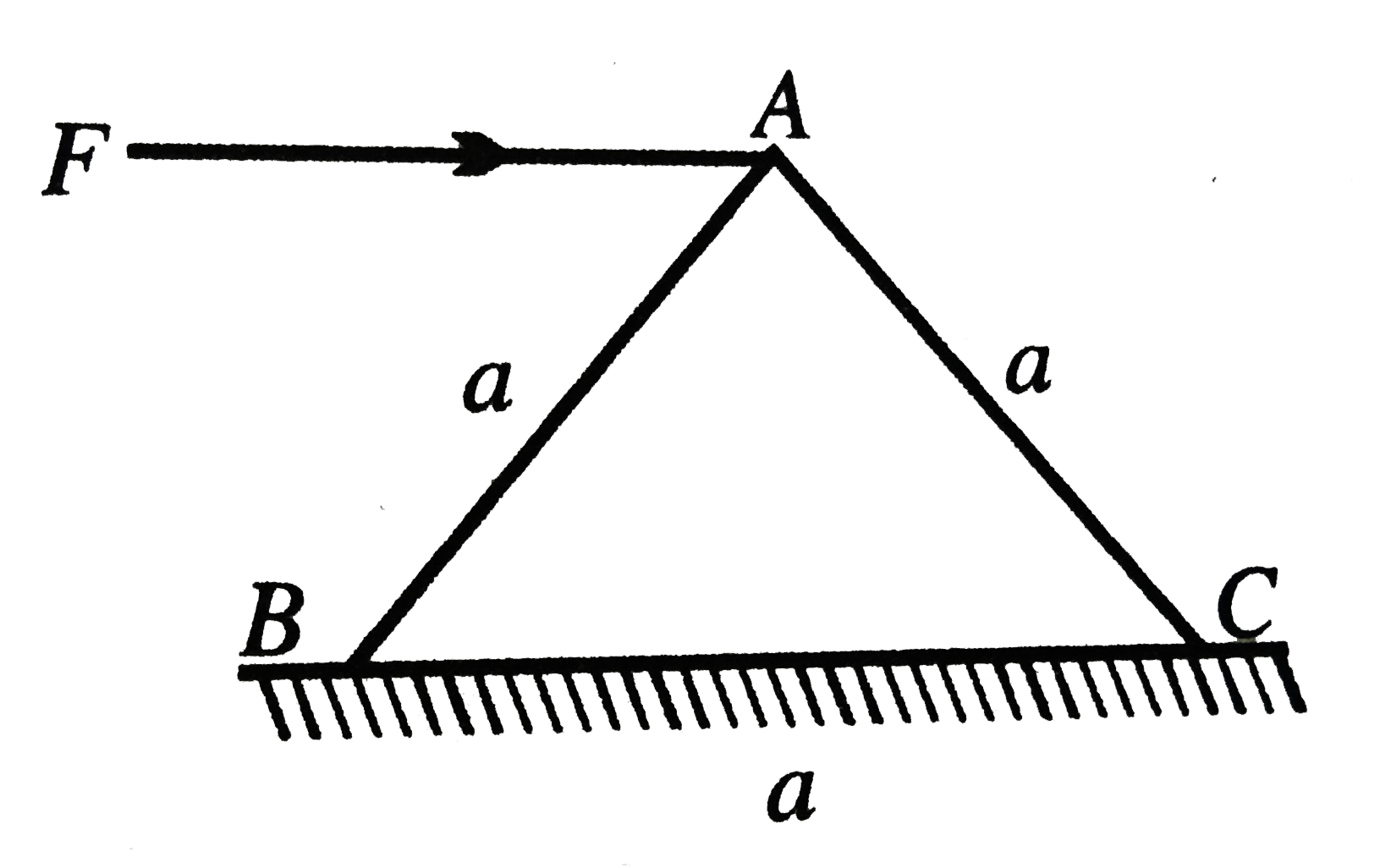 A2√3B13C1√3D12
A2√3B13C1√3D12A cubical box of side length L rests on a rough horizontal surface having coefficient of friction μ. A variable horizontal force F=αt is applied on the top of the block as shown in figure, where α is a constant and t is time. The coefficient of friction is sufficient so that the block does not slide before toppling. The graph between torque due to normal reaction about end B and time before toppling start is
 A
A B
B C
C DNone
DNoneA cubical block of side L rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of frictions sufficienty high so that the block does not slide before toppling, the minimum force required to topple the block is :
 . AinfinitesimalBmg/4Cmg/2Dmg(1−μ)
. AinfinitesimalBmg/4Cmg/2Dmg(1−μ)
A cubical block of edge length 1 m and density 800 kg m−3 rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the block as shown in figure. If the coefficient of friction is sufficiently large so that the block does not slide bofore toppling, then the minimum value of F to topple the block is [Take g = 10 ms−2]

View SolutionA cubical block of side L rests on a rough horizonta surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is

View SolutionA cubical block of side L rests on a rough horizonta surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is

View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the prism as shown in the figure. If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is -
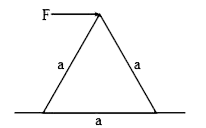
View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with cofficent of friction μ. A horizontal force F is applied on the prism as shown in the figure. If the cofficent of the friction is sufficently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is
View Solution

