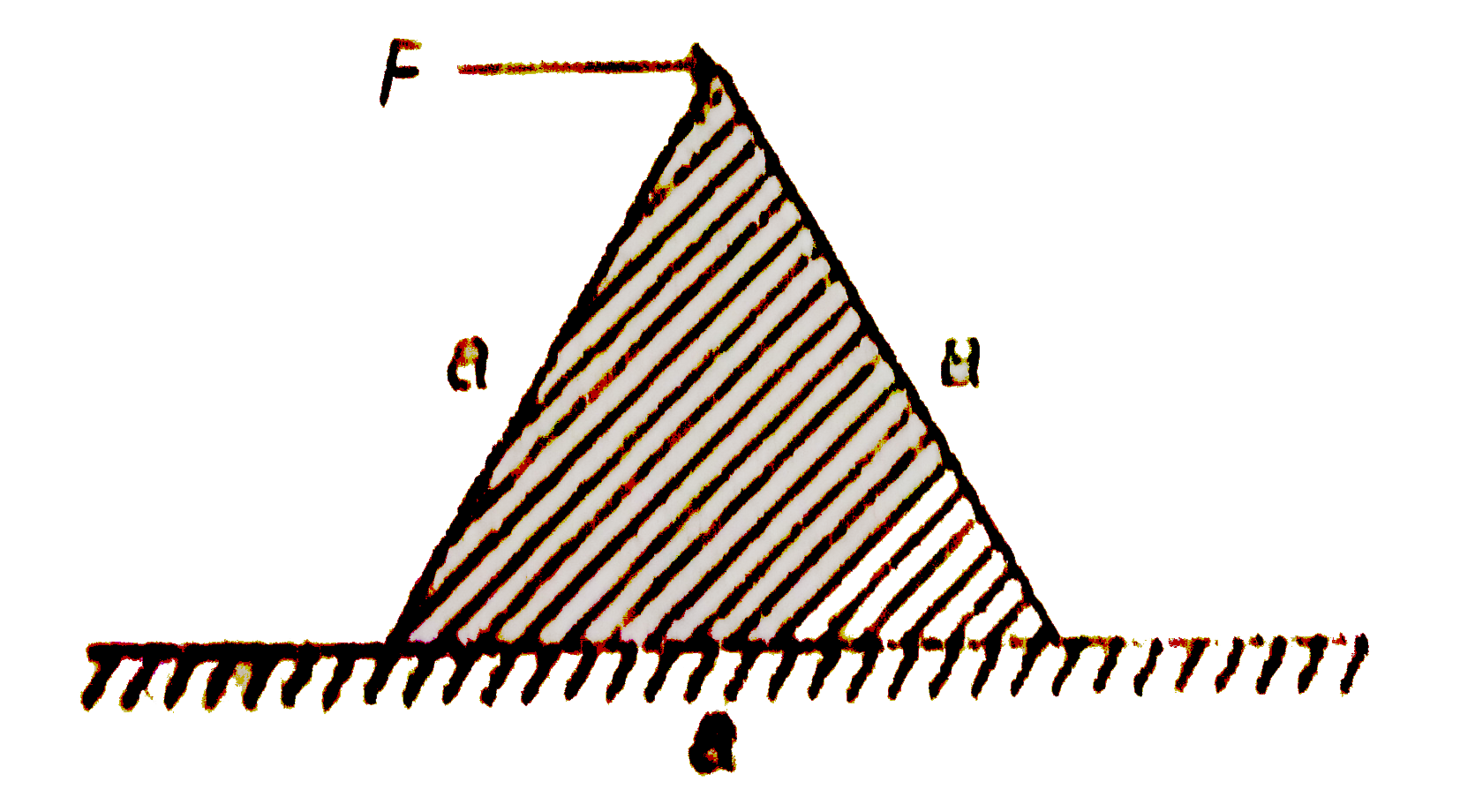
An equilateral prism of mass m rests on a rough horizontal surface with cofficent of friction μ. A horizontal force F is applied on the prism as shown in the figure. If the cofficent of the friction is sufficently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is
(mg)(√3)
mg4
μmg√3
μmg4
The correct Answer is:A
Step by step video, text & image solution for An equilateral prism of mass m rests on a rough horizontal surface with cofficent of friction mu. A horizontal force F is applied on the prism as shown in the figure. If the cofficent of the friction is sufficently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
An equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the prism as shown in the figure. If ihe coefficient of friction is sufficiently high so that the -prism does not slide before toppling, then the minimum force required to topple the prism is mg√n. Find n.
'(##CEN_KSR_PHY_JEE_C09_E01_029_Q16##)'
View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction μ . A horizontal force F is applied on the top of prism as shown in figure. If the coefficient of friction is sufficiently high so that the prism does not slide before topping, the minimum force required to topple the prism is

View Solution
Knowledge Check
An equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the prism as shown in the figure. If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is -
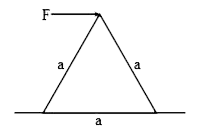 Amg√3Bmg4Cμmg√3Dμmg4
Amg√3Bmg4Cμmg√3Dμmg4An equilateral prism of mass m rests on a rough horizontal surface with cofficent of friction μ. A horizontal force F is applied on the prism as shown in the figure. If the cofficent of the friction is sufficently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is
 A(mg)(√3)Bmg4Cμmg√3Dμmg4
A(mg)(√3)Bmg4Cμmg√3Dμmg4An equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the prism as shown in figure. If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, the minimum force required to topple the prism is
 Amg√3Bmg4Cμmg√3Dμmg4
Amg√3Bmg4Cμmg√3Dμmg4
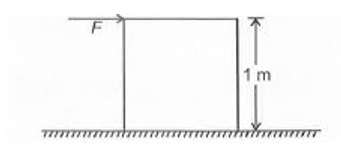
A cubical block of edge length 1 m and density 800 kg m−3 rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the block as shown in figure. If the coefficient of friction is sufficiently large so that the block does not slide bofore toppling, then the minimum value of F to topple the block is [Take g = 10 ms−2]
View SolutionA cubical block of side L rests on a rough horizonta surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is

View SolutionA cubical block of side L rests on a rough horizonta surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is

View SolutionA cubical block of side L rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of frictions sufficienty high so that the block does not slide before toppling, the minimum force required to topple the block is :
 .
.
View SolutionA cubical box of side length L rests on a rough horizontal surface having coefficient of friction μ. A variable horizontal force F=αt is applied on the top of the block as shown in figure, where α is a constant and t is time. The coefficient of friction is sufficient so that the block does not slide before toppling. The graph between torque due to normal reaction about end B and time before toppling start is

View Solution
