A concentric hole of radius R/2 is cut from a thin circular plate of mass M and radius R. The moment of inertia of the remaining plate about its axis will be
1324MR2
1124MR2
1332MR2
1532MR2
The correct Answer is:D
Mass of hole (M')=(MπR2)(πR24)=M4
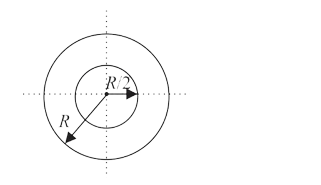
Moment of inertial of remaining plate
=12MR2−12M'(R2)2=1532MR2
Similar Questions
Knowledge Check
A hole of radius R/2 is removed from a thin circular plate of radius R and mass M. The moment of inertia of the remaining plate about an axis through centre O and perpendicular to the plane of the plate is
 A3MR232B3MR213C1332MR2D3213MR2
A3MR232B3MR213C1332MR2D3213MR2Four holes of radius R are cut from a thin square plate of side 4R and mass M. The moment of inertia of the remaining portion about z-axis is :
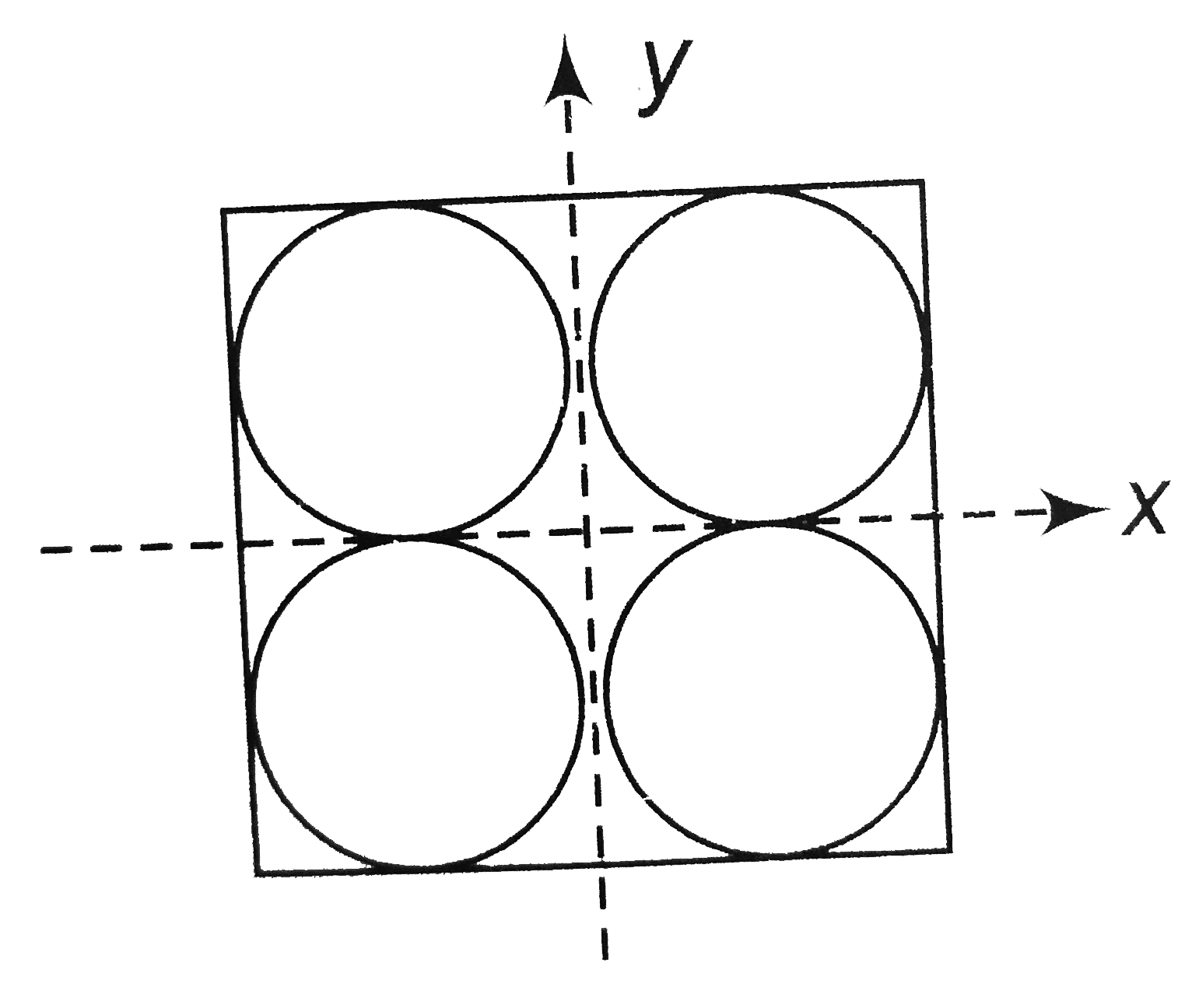 .Aπ12MR2B(43−π4)MR2C(83−10π16)MR2D(43−π6)MR2.
.Aπ12MR2B(43−π4)MR2C(83−10π16)MR2D(43−π6)MR2.A rectangular piece of dimension l×b is cut out of central portion of a uniform circular disc of mass m and radius r. The moment of inertia of the remaining piece about an axis perpendicular to the plane of the disc and passing through its centre is :
Am[r2−lb6πr2(l2+b2)Bm2[r2−lb6πr2(l2+b2)]Cm2[r2−(l2+b2)6]Dnot determinable as mass of the rectangular piece is not given
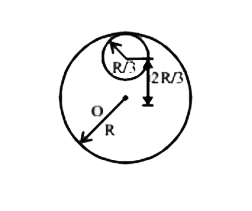
A circular of radius R has mass 9m . A hole of radius R3 is cut from it as shown in figure. The moment of inertia of the remaining part about an axis passing through centre 0 of the disc and perpendicular of the plane of disc is xmR2 .Find value of x
View SolutionA disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :
View SolutionA hole of radius R/2 is cut from a thin circular plate of raduis R as shown in the figure. If the mass of the remaining plate is M, then find moment of inertia of the plate about an axis through O perpendicular to plane

View SolutionFrom a disc of radius R, a concentric circular portion of radius r is cut out so as to leave an annular disc of mass M. The moment of inertia of this annular disc about the axis perpendicular to its plane and passing through its centre of gravity is
View SolutionFrom a circular disc of radius R and 9M , a small disc of mass M and radius R3 is removed concentrically .The moment of inertia of the remaining disc about and axis perpendicular to the plane of the disc and passing through its centre is
View Solution