ABC is a triangular park with AB = AC = 100 metres. A vertical tower is stiuated at the mid-point of BC. If the angles of elevation of the top of the tower at A and B are cot1(3√2) and cosec−1(2√2) respectively,then the height of the tower (in meters) is :
1003√3
25
20
10√5
The correct Answer is:C
Let h(m) be the height of the tower
Say BM=d
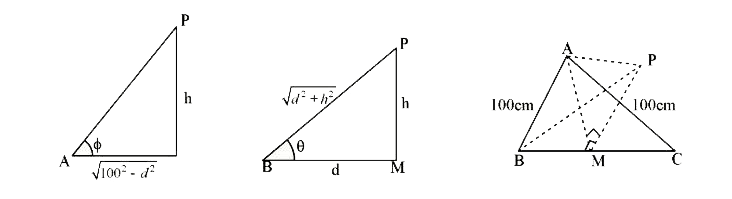
θ=cosec−12√2
2√2=√d2−d2h
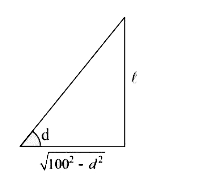
cotϕ=√(100)2−d2h
3√2=√(100)2−d2h
18h2=1002−d2...........(2)
Put the values of d2 from (1) and (2)
18h2=1002−7h2⇒25h2=100×100
h=20 m
Similar Questions
ABC is a triangular park with AB = AC = 100 metres. A vertical tower is situated at the mid-point of BC. If the angles of elevation of the top of the tower at A and B are cot−1(3√2) and cosec−1(2√2) respectively, then the height of the tower (in metres) is :
View SolutionABC is a triangular park with AB = AC = 100 m. A block tower is situated at the midpoint of BC.The angles of elevation of the top of the tower at A and B are cot−1(3.2) and cosec−1(2.6) respectively.The height of the tower is:
View Solution
Knowledge Check
ABC is a triangular park with AB = AC = 100 m. A vertical tower is situated at the mid-point of BC. If the angles of elevation of the top of the tower at A and B are cot−1(3√2) and cosec−1(2√2) respectively, then the height of the tower (in m) is
A25B20C10√5D1003√3ABC is a triangular park with AB+AC=100 m. a clock tower is situated at the mid-point of BC. The angles of elevation of the top of the tower at A and B are cot−1 3⋅2andcosec−1 2⋅6 respectively. The height of the tower is
A16 mB25 mC50 mDNoneThere are three points A, B and C horizontal plane, such that AB=AC=100m a varticaly tower is placed on the midpoint of BC, such that angle of elevation of the top of the tower from A is cot−1(3√2) and that from B is cosec−1(2√2) then the height of the tower is
A25B10C100√3D20
ABC is a triangular park with AB = AC = 100 m. A block tower is situated at the midpoint of BC.The angles of elevation of the top of the tower at A and B are cot−1(3.2) and cosec−1(2.6) respectively.The height of the tower is:
View SolutionABC is a triangular park with AB=AC=100m. A clock tower is situated at the mid-point of BC. The angle of elevation, If the top of the tower at A and B are cot−13.2 and cosec−12.6, respectively. The height of the tower is
View SolutionABC is a triangular park with AB=AC=100m. A Television tower stands at the mid point of BC. The angles of elevations of the top of tower at A,B,C are 45∘,60∘,60∘ respectively Then the height of tower is
View SolutionPQR is a triangular park with PQ=PR=200m . A T.V tower stands at the mid-point of QR. If the angles of elevation of the top of the tower at P , Q and R respectively 45∘ , 30∘ and 30∘ then the height of the tower in m is
View SolutionThe shadow of a tower is √3 times its height .Then the angle of elevation of the top of the tower is
View Solution
