ABC is a triangular park with AB = AC = 100 m. A vertical tower is situated at the mid-point of BC. If the angles of elevation of the top of the tower at A and B are $\cot^{- 1} (3 \sqrt{2})$ and $\cos e c^{- 1} (2 \sqrt{2})$ respectively, then the height of the tower (in m) is

A

25

B

20

C

$10 \sqrt{5}$

D

$\frac{100}{3 \sqrt{3}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Given ABC is a triangular park with AB = AC = 100 m. A vertical tower is situated at the mid-point of BC.
Let the height of the tower is h m.
Now, according to given information, we have the following figure.

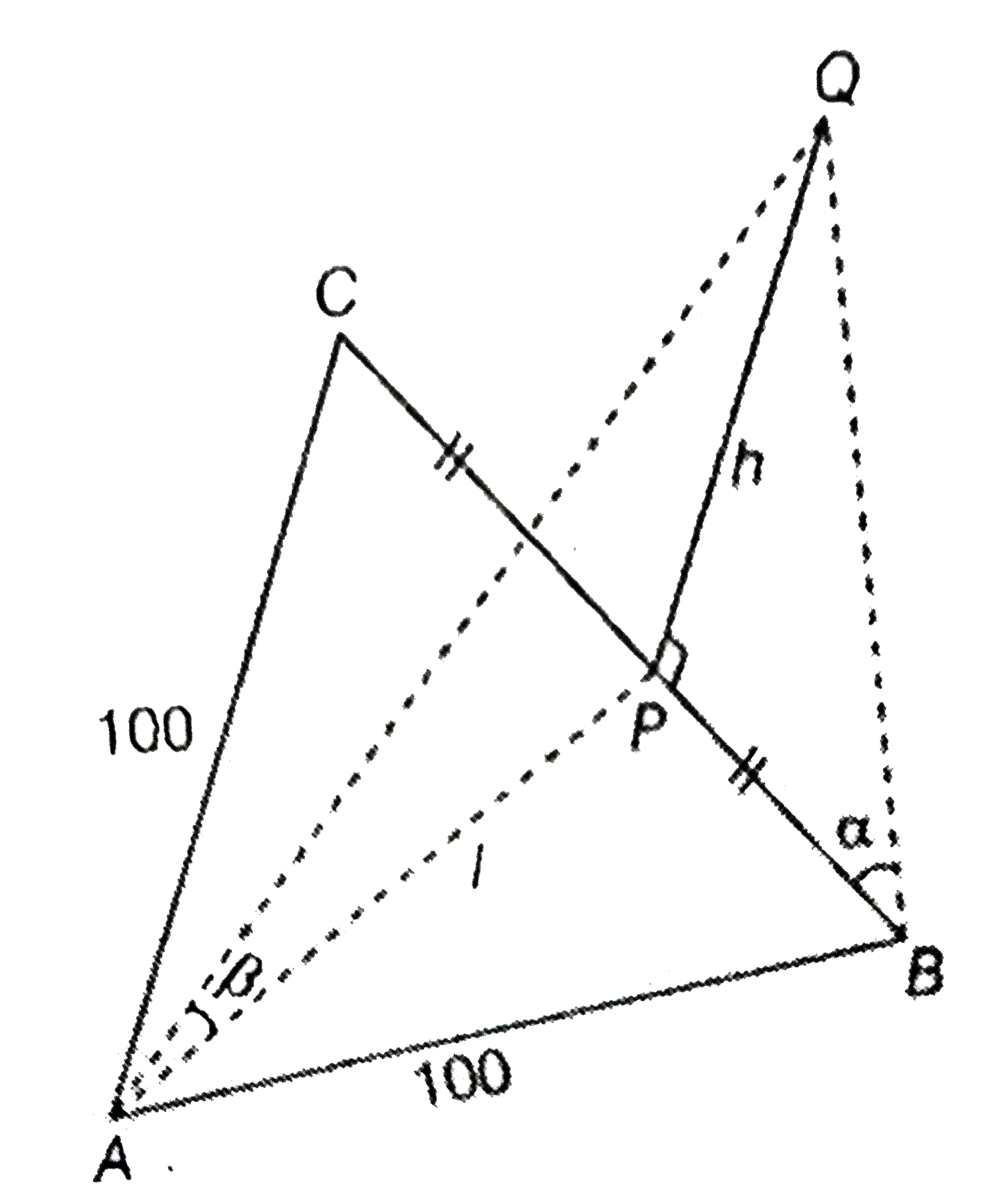
From the figure and given information, we have
$β = \cot^{- 1} (3 \sqrt{2})$
and $α = \cos e c^{- 1} (2 \sqrt{2})$
Now, in $Δ Q P A$ ,
$\cot β = \frac{l}{h}$
$\Rightarrow l = (3 \sqrt{2}) h ...(i)$
and in $Δ B P Q, \tan α = \frac{h}{B P}$
$\Rightarrow \cot α = \frac{B P}{h} = \frac{\sqrt{(100^{2}) - l^{2}}}{h}$
$[∵ p is mid-point of isosceles Δ A B C, A P ⊥ B C]$
$\Rightarrow h^{2} \cot^{2} α = {(100)}^{2} - l^{2}$
$\Rightarrow h^{2} (\cos e c^{2} α - 1) = {(100)}^{2} - {(3 \sqrt{2} h)}^{2} [from Eq. (i)]$
$\Rightarrow h^{2} (8 - 1) = {(100)}^{2} - 18 h^{2}$
$\Rightarrow 25 h^{2} = {(100)}^{2}$
$\Rightarrow h^{2} = {(\frac{100}{5})}^{2} \Rightarrow h = 20 m$

|

Updated on:21/07/2023

Class 12 MATHS TRIGONOMETRICAL RATIOS AND IDENTITIES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
ABC is a triangular park with AB = AC = 100 metres. A vertical tower is stiuated at the mid-point of BC. If the angles of elevation of the top of the tower at A and B are ${cot}^{- 1} (3 \sqrt{2})$ and $cos e c^{- 1} (2 \sqrt{2})$ respectively,then the height of the tower (in meters) is :
A $\frac{100}{3 \sqrt{3}}$
B $10 \sqrt{5}$
C20
D25
Question 2 - Select One
ABC is a triangular park with AB+AC=100 m. a clock tower is situated at the mid-point of BC. The angles of elevation of the top of the tower at A and B are ${cot}^{- 1} 3 \cdot 2 and {cosec}^{- 1} 2 \cdot 6$ respectively. The height of the tower is
A16 m
B25 m
C50 m
DNone
Question 3 - Select One
There are three points A, B and C horizontal plane, such that $A B = A C = 100$ m a varticaly tower is placed on the midpoint of BC, such that angle of elevation of the top of the tower from A is ${cot}^{- 1} (3 \sqrt{2})$ and that from B is $cos e c^{- 1} (2 \sqrt{2})$ then the height of the tower is
A $25$
B $10$
C $\frac{100}{\sqrt{3}}$
D $20$

IIT JEE PREVIOUS YEAR-TRIGONOMETRICAL RATIOS AND IDENTITIES-HEIGHT AND DISTANCE

Home
Ask Doubt
Profile