A solid sphere of mass M and radius R is divided into two unequal parts. The first part has a mass of and is converted into a uniform disc of radius 2R. The second part is converted into a uniform solid sphere. Let be the moment of inertia of the disc about its axis and be the moment of inertia of the new sphere about its axis. The ratio is equal to __________ .
The correct Answer is:140
(Radius of new sphere )
Similar Questions
A solid sphere of mass M and radius R is divided into two unequal parts. The first parts has a mass of 7M8 and is converted into a uniform disc of radius 2R. The second part is converted into a uniform solid sphere. Let I1 be the moment of inertia of the uniform disc about its axis and I2 be the moment of inertia of the sphere made from remaining part about its axis. The ratio I1/I2 is 140x. Find the value of x.
View SolutionA sphere of mass 10 kg and radius 0.5 m rotates about a tangent. The moment of inertia of the solid sphere about tangent is
View Solution
Knowledge Check
A solid sphere of mass m& rdius R is divided in two parts of m mass 7m8&m8, and converted to a disc of radius 2R& solid sphere of radius 'r' respectively. Find I1I2 , If I1&I2 are moment of inertia of disc & solid sphere respectively
A160B140C240D120Moment of inertia of a disc of mass 'M' and radius 'R' about the diameter is
AMR22BMR24CMR23DMR212A solid sphere of radius R has moment of inertia l about its diameter. What will be moment of inertia of a shell of same mass and same radius about its diameter?
A35lB53lC23lD25l
If the radius of gyration of a solid disc of mass 10 kg about an axis is 0.40 m, then the moment of inertia of the disc about that axis is
View SolutionThe moment of inertia of a solid sphere of mass M and radius R about its diameter is I. The moment of inertia of the same sphere about a tangent parallel to the diameter is
View SolutionTwo spheres of same mass and radius are in contact with each other. If the moment of inertia of a sphere about its diameter is I, then the moment of inertia of both the spheres about the tangent at their common point would be
View SolutionThe moment of inertia of a disc of mass M and radius R about a tangent to its rim in its plane is
View SolutionThe diagram shows a uniform disc of mass M & radius 'a', if the moment of inertia of the disc about the axis XY is I, its moment of inertia about an axis through O and perpendicular to the plane of the disc is
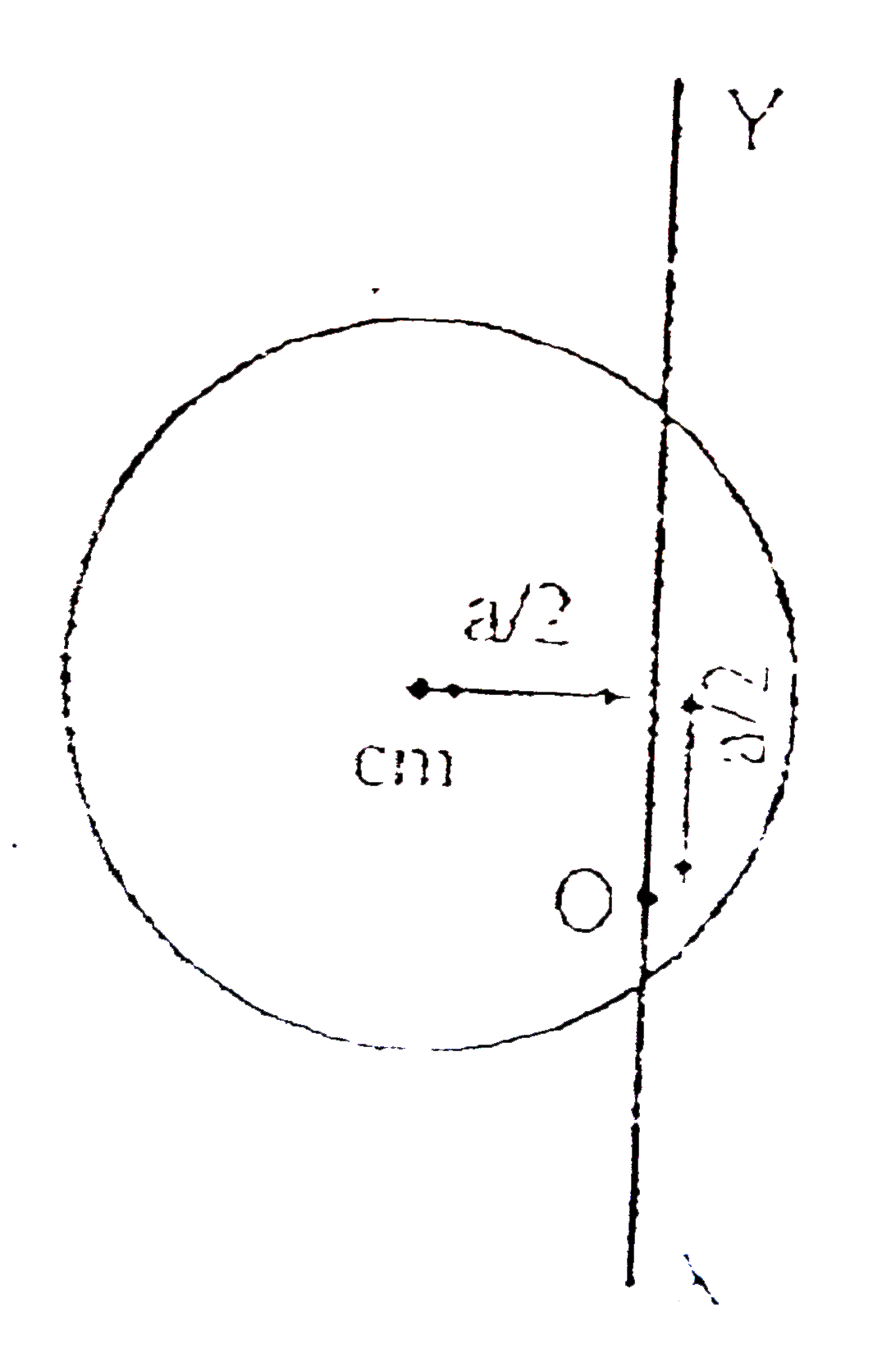
View Solution

