The height of a right circular cylinder of maxium volume inscirbed in a sphere of radius 3 is

$\sqrt{6}$

$\sqrt{3}$

$\frac{2}{3} \sqrt{3}$

$2 \sqrt{3}$

Video Solution

Text Solution

Verified by Experts

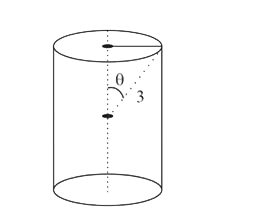
$h = 2 (3 cos θ)$
$r = 3 sin θ, v = π r^{2} h, = π 9 {sin}^{2} θ . 6 cos θ$
$V = 54 π sin 2 θ cos θ, \frac{d v}{d θ} = 0$
$\Rightarrow 2 sin θ {cos}^{2} θ - {sin}^{3} θ = 0 \Rightarrow 2 s (1 - s^{2}) - s^{3} = 0 \Rightarrow 2 s - 2 s^{3} - s^{3} = 0$
$\Rightarrow 2 s - 3 s^{3} = 0 \Rightarrow s = 0 or 2 - 3 s^{2} = 0$
$s = \pm \sqrt{\frac{2}{3}} ∴ cos θ = \sqrt{1 - \frac{2}{3}} = \frac{1}{\sqrt{3}}$
$h = 6 (\frac{1}{\sqrt{3}}), h = 2 \sqrt{3}$

Updated on:21/07/2023

The height of the cylinder of max. volume that can be inscribed in a sphere of radius a is
A $\frac{2 a}{\sqrt{3}}$
B $\frac{a}{\sqrt{2}}$
C $\frac{5 a}{4}$
DNone
The height of the cylinder of the greatest volume that can be inscribed in a sphere of radius 3 is
A $3 \sqrt{3}$
B $2 \sqrt{3}$
C $\sqrt{3}$
D $\sqrt{2}$
Each of the radius of the base and the height of a right circular cylinder is increased by 10%. The volume of the cylinder is increased by
A $3.31 %$
B $14.5 %$
C $33.1 %$
D $19.5 %$