Assertion: For a particle moving in a straight line velocity (v in m//s) of the particle in terms of time (t in sec) is given by v=t2−6t+8. Then the speed of the particle is minimum at t=2sec
Reason: For a particle moving in a straight line line velocity v at any time t may be minimum or may be maximum when dvdt=0.
Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1.
Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1.
Statement-1 is True, Statement-2 is False.
Statement-1 is False, Statement-2 is True
The correct Answer is:B
Step by step video, text & image solution for Assertion: For a particle moving in a straight line velocity (v in m//s) of the particle in terms of time (t in sec) is given by v = t^2 - 6t + 8. Then the speed of the particle is minimum at t = 2 sec Reason: For a particle moving in a straight line line velocity v at any time t may be minimum or may be maximum when (dv)/(dt) = 0. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBook:MOTIONChapter:KINEMATICSExercise:EXERCISE 2 OBJECTIVE PROBLEMS (Level-2)
Explore 26 Videos
- KINEMATICSBook:MOTIONChapter:KINEMATICSExercise:EXERCISE 3 SUBJECTIVE PROBLEMS (Level-1)
Explore 20 Videos
- KINEMATICSBook:MOTIONChapter:KINEMATICSExercise:EXERCISE 1 OBJECTIVE PROBLEMS
Explore 103 Videos
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBook:MOTIONChapter:HYDROSTATIC, FLUID MECHANICS & VISCOSITYExercise:EXERCISE -3 (SECTION-B) PREVIOUS YEAR PROBLEM
Explore 7 Videos
- KINETIC THEORY OF GASES Book:MOTIONChapter:KINETIC THEORY OF GASES Exercise:EXERCISE-3 SECTION-B
Explore 16 Videos
Similar Questions
Velocity (in m/s) of a particle moving in a straight line given by v=(t2−2t1). Match Table-1 with Table -2
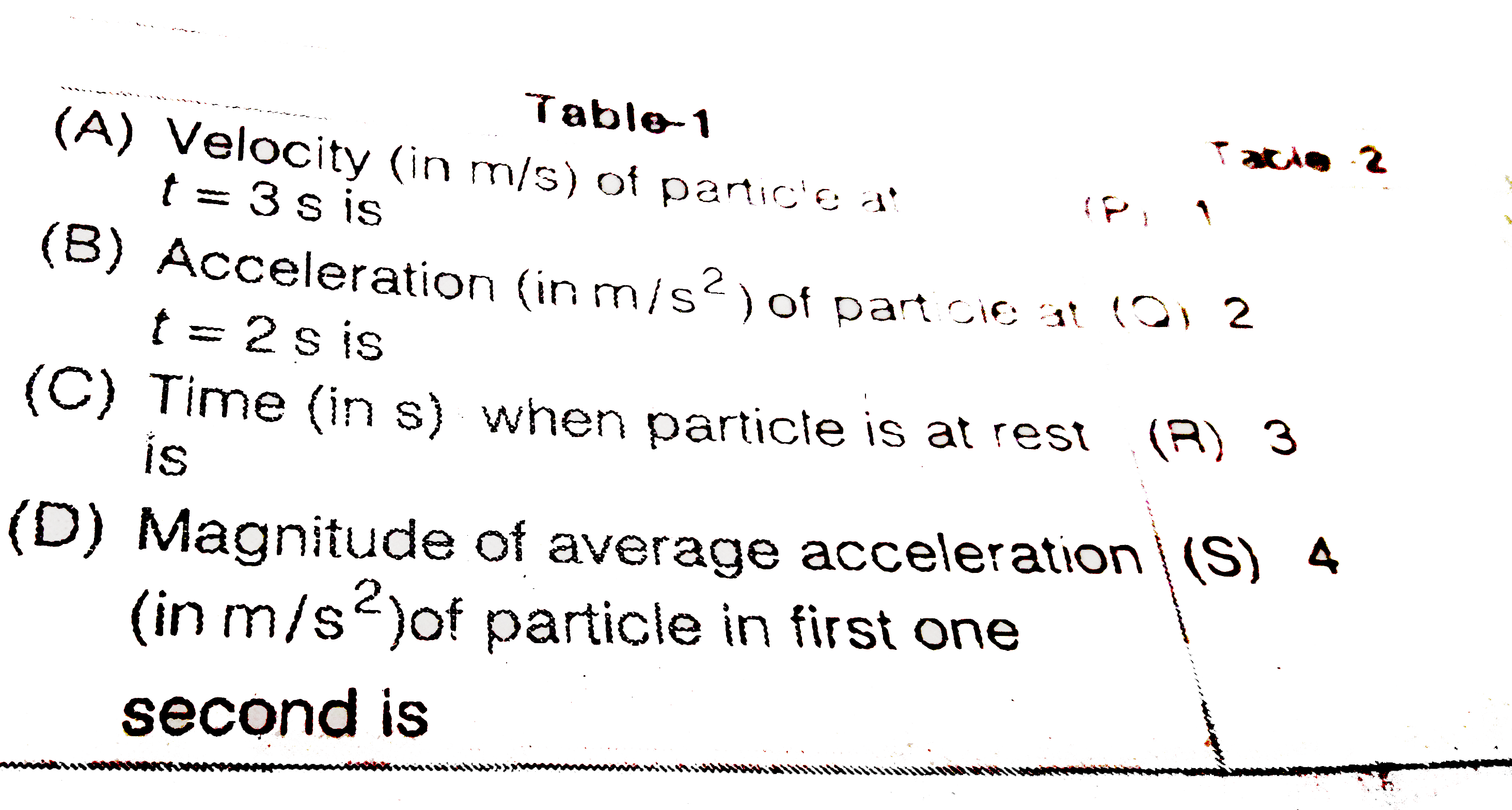
View SolutionA particle is moving in a straight line and its velocity varies with its displacement as v=√4+4s m/s. Assume s=0 at t=0. find the displacement of the particle in metres at t=1s.
View Solution
Knowledge Check
For a particle moving in a straight line, the displacement of the particle at time t is given by
S=t3−6t2+3t+7
What is the velocity of the particle when its acceleration is zero?A−9ms−1B−12ms−1C3ms−1D42ms−1The position of a particle moving on a straight line depends on time t as
x=(t+3)sin(2t)AIts velocity at the initial moment is 6 m/sBIts acceleration at the initial is −8m/s2CIt has velocity of 3 m/s at t=π2 secDIt has an acceleration of 2m/s2 at t=π4 secA particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
AAverage velcotu is 25/3ms−1BAverage speed is 10ms−1.CAverage velcotu is 5/3ms−1DAcceleration is 4ms−2 at t=o
The velocity (V) of a particle (in cm/s) is given in terms of time (t) in sec by the equation V=at+bc+t. The dimensions of a, b and c are
View SolutionThe fig. shows the v−t graph of a particle moving in straight line. Find the time when particle returns to the starting point.

View SolutionA particle moves along a straight line such that its displacement at any time t is given by s=3t3+7t2+14t+5. The acceleration of the particle at t=1s is
View SolutionPosition of a particle moving along a straight line is given by x=2t2+t . Find the velocity at t = 2 sec.
View SolutionThe x−t graph of particle moving along a straight line is shown in figure

The v−t graph of the particles is correctly shown by
View Solution

