A man standing on a road has to hold his umbrella at 300 with the vertical to keep the rain away. The throws the umbrella and starts running at 10 km/h. He finds that raindrops are hitting his head vertically. Find the speed of raindrops with respect to a. the road, b. the moving man.
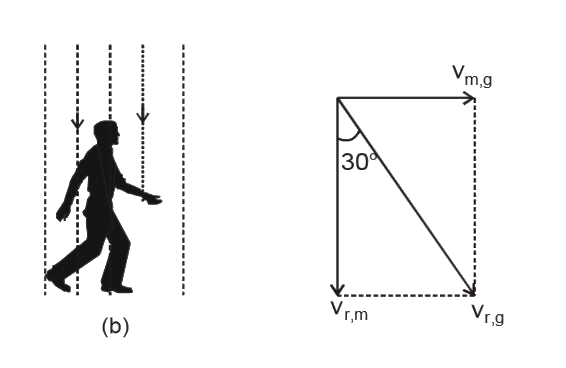
here ¯vrg=velocity of the rain with respect to the ground
¯vmg=velocity of the man with respect to the ground and ¯vrm=velocity fo the rain with respect to the man.
We have ¯vrg=¯vrm+¯vmg
Taking horizontal components, equation (i) gives
vrgsin30∘=umg=10km/h or v,g
=10km/hsin30∘=20km/h
Taking vertical components, equation (i) gives
vrgcos30∘=vrm or vrm=(20km/h)√32
10√3km/h
Topper's Solved these Questions
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 1 OBJECTIVE PROBLEMS
103 Videos
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 2 OBJECTIVE PROBLEMS
75 Videos
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - EXERCISE -3 (SECTION-B) PREVIOUS YEAR PROBLEM
7 Videos
- KINETIC THEORY OF GASES BOOK - MOTIONCHAPTER - KINETIC THEORY OF GASES EXERCISE - EXERCISE-3 SECTION-B
16 Videos
Similar Questions
A man standing on a road has to hold his umbrella at 300 with the veetical to keep the rain away. The throws the umbrella and starts running at 10 km/h. He finds tht raindrops are hitting his head vertically. Find the speed of raindrops with respect to a. the road, b. the moving man.
View SolutionA man standing on a road has to hold his umbrella at 30∘ with the vertical to keep the rain away. He throws the umbrella and starts running at 10km/hr. He finds that rain drop are hitting his head vertically. Find the speed of rain drops with respect to (a) road (b) the moving man.
View Solution
Knowledge Check
A man running with velocity 3m/s finds that raindrops are hitting him vertically with a speed of 4m/s.
Magnitude of velocity of the raindrops isA3m/sB4m/sC5m/sD6m/sA man running with velocity 3m/s finds that raindrops are hitting him vertically with a speed of 4m/s.
Raindrops are falling at an angle θ with the vertical. Value of θ isA37∘B53∘C45∘D60∘Statement -1 : A man standing on the ground has to hold his umbrella at an angle θ with the vertical to protect himself from rain. It is possible that the man now starts running on the ground with certain speed, but he still has to hold his umbrella at angle θ with the vertical to protect himself from rain.
Statement -2 : Vertical component of velocity of rain w.r.t man does not change. if he starts running on a horizontal ground.AStatement -1 is Ture, statement -2 is Ture, Statement -2 is a correct explanation for statement -1 .BStatement -1 is True, statement -2 is True, statement - 2 is NOT a correct explanation for statement -3CStatement -1 is True, Statement -2 si FalseDStatement -1 is False ,Statement -2 is True.
A person standing on a road has to hold his umbrella at 600 with the verticcal to keep the rain away. He throws the umbrella an starts running at 20ms−1. He finds that rain drops are hitting his head vertically. Find the speed of the rain drops wigh respect to (a) the road (b) the moving person.
View SolutionA person standing on a road has to hold his umbrellat at 45∘ with the vertical to deep the rain away . He throws the umbtella and starts running at 30ms−1 . He find that the rain drops are hitting his head vertically. Fing the speed of the rain drops with respect to (a) road (b) the moving person.
View SolutionTo a stationary man, rain appears to be falling at his back at an angle 30∘ with the vertical. As he starts moving forward with a speed of 0.5ms−1, he finds that the rain is falling vertically.
The speed of rain with respect to the moving man is.
View SolutionA man running on the horizontal road at 8kmh−1 find the rain appears to be falling vertically. He incresases his speed to 12kmh−1 and find that the drops make angle 302 with the vertical. Fin dthe speed and direction of the rain with respedt to the road.
View SolutionTo a stationary man, rain appears to be falling at his back at an angle 30∘ with the vertical. As he starts moving forward with a speed of 0.5ms−1, he finds that the rain is falling vertically.
The speed of rain with respect to the stationary man is.
View Solution
