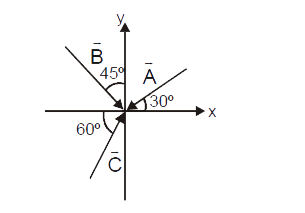
Three vectors $\to A, \to B, \to C$ are shown in the figure. Find angle between
(i) $\to A$ and $\to B$ (ii) $\to B$ and $\to C$ (iii) $\to A$ and $\to C$ .

Video Solution

Text Solution

Verified by Experts

To find the angle between two vectors we connect the tails of the two vectors. We can shift $\to B & \to C$ such that tails of $\to A, \to B, and \to C$ are connected as shown in figure.

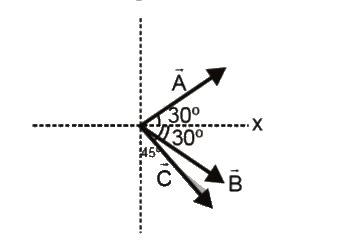
Now we can easily observe that angle between $\to A and \to B is 60^{\circ}, \to B and \to C$ is $15^{\circ}$ and between $\to A$ and $\to C$ is $75^{\circ}$ .

|

Updated on:21/07/2023

Class 12 PHYSICS VECTOR & CALCULUS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
Three vectors $\to a, \to b, \to c$ are such that $\to a \times \to b = 4 (\to a \times \to c)$ and $| \to a | = ∣ ∣ \to b ∣ ∣ =$ and $| \to c | = \frac{1}{4}$ . If the angle between $\to b$ and $\to c$ is $\frac{π}{3}$ then $\to b$ is
A $\to a + 4 \to c$
B $\to a - 4 \to c$
C $4 \to c - \to a$
D $2 \to c - \to a$

MOTION-VECTOR & CALCULUS-EXERCISE -4 (LEVEL - II) PREVIOUS YEAR

Home
Ask Doubt
Profile