The vector →P makes 120∘ with the x-axis and vector Q makes 30° with the y-axis. What is their resultant?
P+Q
P−Q
√P2+Q2
√P2−Q2
The correct Answer is:A
To find the resultant of the vectors →P and →Q, we will follow these steps:
Step 1: Understand the Angles
- Vector →P makes an angle of 120∘ with the x-axis.
- Vector →Q makes an angle of 30∘ with the y-axis.
Step 2: Determine the Angles with Respect to the X-Axis
- The angle →P makes with the x-axis is 120∘.
- To find the angle →Q makes with the x-axis, we can calculate it as follows:
Angle of →Q with x-axis=90∘−30∘=60∘
Step 3: Express the Vectors in Component Form
- The components of vector →P:
→P=Pcos(120∘)^i+Psin(120∘)^j
Using cos(120∘)=−12 and sin(120∘)=√32:
→P=P(−12)^i+P(√32)^j=−P2^i+P√32^j
- The components of vector →Q:
→Q=Qcos(60∘)^i+Qsin(60∘)^j
Using cos(60∘)=12 and sin(60∘)=√32:
→Q=Q(12)^i+Q(√32)^j=Q2^i+Q√32^j
Step 4: Add the Vectors
- The resultant vector →R=→P+→Q:
→R=(−P2+Q2)^i+(P√32+Q√32)^j
Simplifying gives:
→R=(Q−P2)^i+((P+Q)√32)^j
Step 5: Calculate the Magnitude of the Resultant
- The magnitude of the resultant vector R is given by:
R=
⎷(Q−P2)2+((P+Q)√32)2
Simplifying:
R=12√(Q−P)2+3(P+Q)2
Step 6: Conclusion
- The resultant vector →R can be expressed in terms of its components or its magnitude, depending on the values of P and Q.
- Vector →P makes an angle of 120∘ with the x-axis.
- Vector →Q makes an angle of 30∘ with the y-axis.
- The angle →P makes with the x-axis is 120∘.
- To find the angle →Q makes with the x-axis, we can calculate it as follows:
Angle of →Q with x-axis=90∘−30∘=60∘
- The components of vector →P:
→P=Pcos(120∘)^i+Psin(120∘)^j
Using cos(120∘)=−12 and sin(120∘)=√32:
→P=P(−12)^i+P(√32)^j=−P2^i+P√32^j
→Q=Qcos(60∘)^i+Qsin(60∘)^j
Using cos(60∘)=12 and sin(60∘)=√32:
→Q=Q(12)^i+Q(√32)^j=Q2^i+Q√32^j
- The resultant vector →R=→P+→Q:
→R=(−P2+Q2)^i+(P√32+Q√32)^j
Simplifying gives:
→R=(Q−P2)^i+((P+Q)√32)^j
- The magnitude of the resultant vector R is given by:
R=
⎷(Q−P2)2+((P+Q)√32)2
Simplifying:
R=12√(Q−P)2+3(P+Q)2
- The resultant vector →R can be expressed in terms of its components or its magnitude, depending on the values of P and Q.
Topper's Solved these Questions
Similar Questions
A vector →A makes an angle of 20∘and→B makes an angle of −−→110∘ with the X-axis. The magnitude of these vectors are 3 m and 4 m respectively.Find the resultant
View SolutionA resultant of two vectors makes 30∘ with one vector and 45∘ with the other. Find the two vectors if the resultant has the magnitude 15∘
View Solution
Knowledge Check
A force →F1 of magnitude 9 N makes an angle of 30∘ with the X-axis. Another force →F2 of magnitude 12 N, makes an angle of 120∘ with the X-axis. What is the magnitude of the resultant force ?
A7.5 NB10 NC12.5 ND15 NAn electron enters a region that contains a magnetic field directed into the page as shown. The velocity vector of the electron makes an angle of 30∘ with the +y axis. What is the direction of the magnetic force on the electron when it enters the field ?
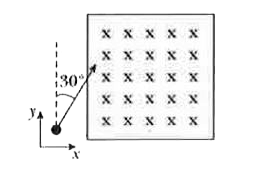 AUp, out of the pageBAt an angle of 30∘ below the positive x axisCAt an angle of 30∘ above the positive x axisDAt an angle of 60∘ below the positive x axis
AUp, out of the pageBAt an angle of 30∘ below the positive x axisCAt an angle of 30∘ above the positive x axisDAt an angle of 60∘ below the positive x axisA vector a makes 30∘ and b makes 120∘ angle with the x-axis. The magnitude of these vectors are 3 unit and 4 unit, respectively. The magnitude of resultant vector is
A3 unitB4 unitC5 unitD1 unit
A vector →A makes an angle 30∘ with the Y-axis in anticlockwise direction. Another vector →B makes an angle 30∘ with the x-axis in clockwise direction. Find angle between vectors →A and →B.
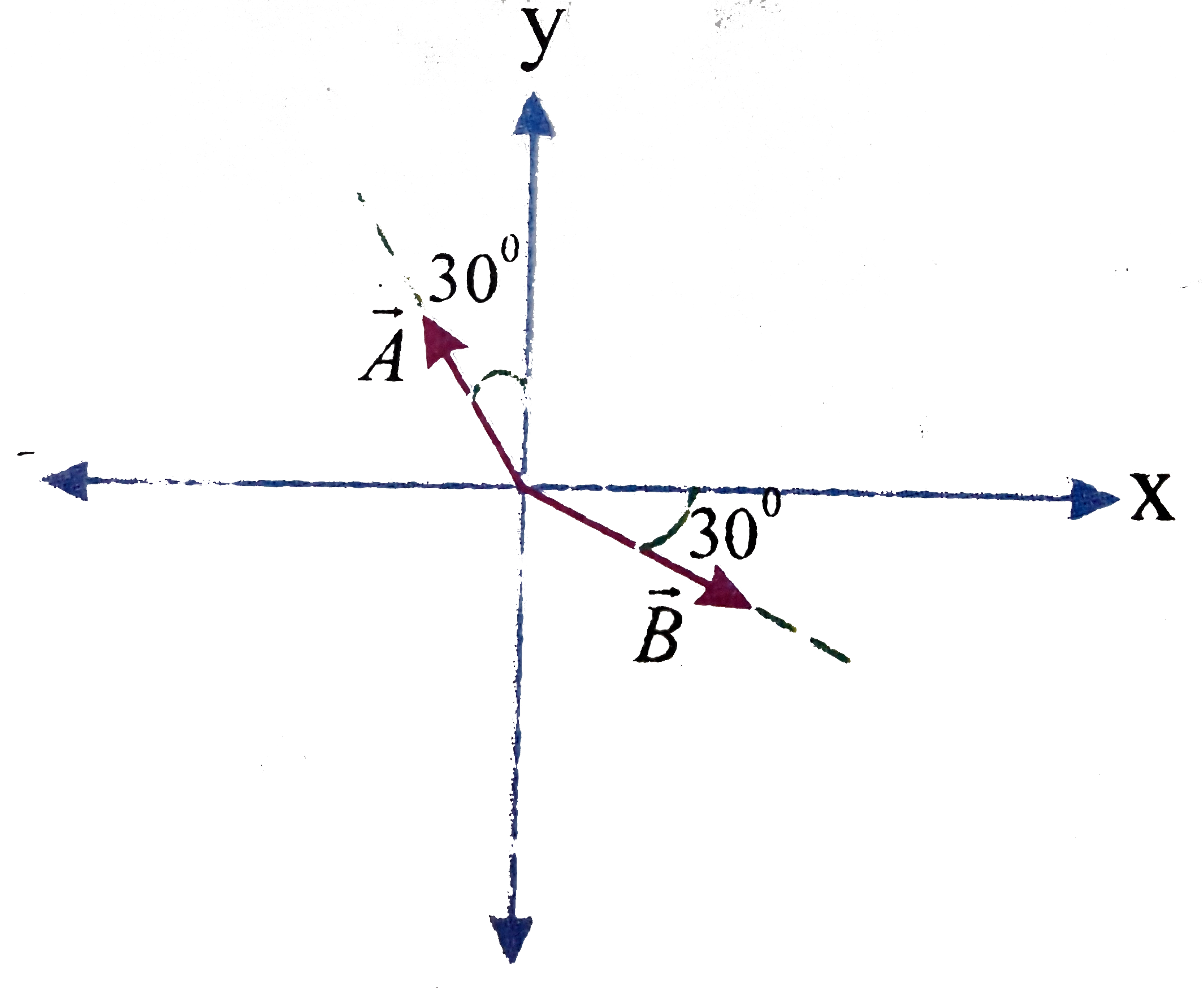
View SolutionTwo vectors (→a and →b) have equal magnitudes of 12 units. These vectors are making angles 30∘ and 120∘ with the x-axis respectively. Their sum is →r .Then the x and y components of r are
View SolutionA vector →A and →B make angles of 20∘ and 110∘ respectively with the X-axis. The magnitudes of these vectors are 5m and 12m respectively. Find their resultant vector.
View SolutionFind the angle that the vector A=2ˆi+3ˆj−ˆk makes with y-axis.
View SolutionThe resultant of two vectors makes an angle of 60∘ with one vector and 30∘ with one other. If the magnitude of resultant is 25, the two vectors are of magnitude
View Solution
