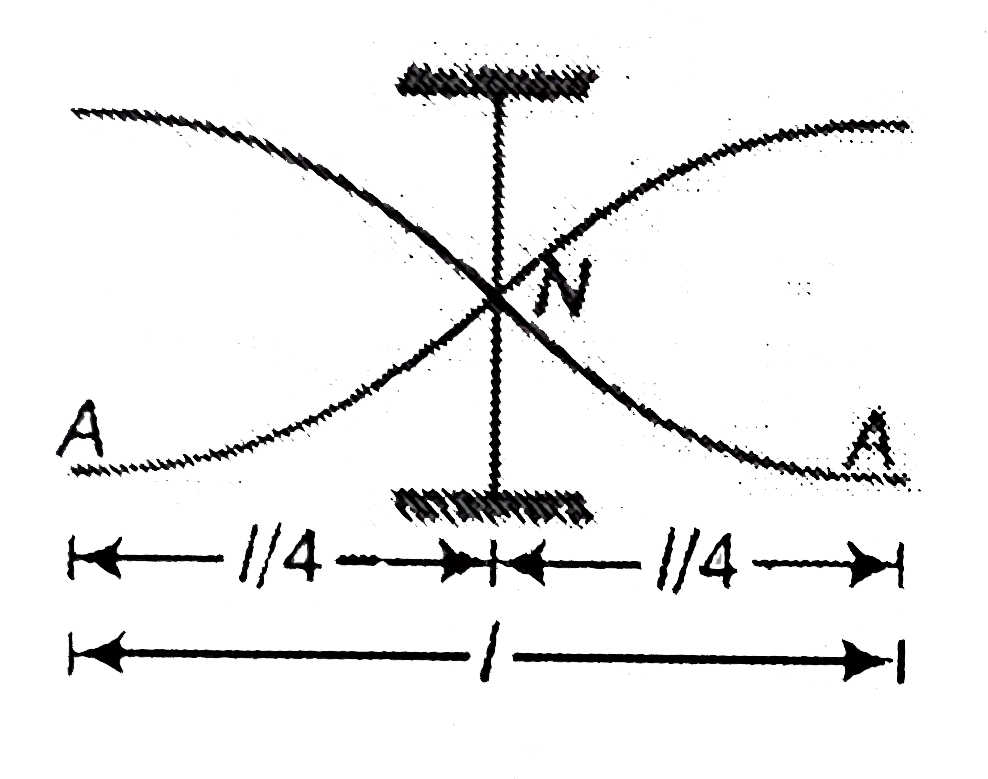
A steel rod 100 cm long is clamped at its middle. The fundamental frequency of loungitudinal vibrations of the fundamental frequency of longitudinal vibrations of the rod are given to be 2.53 KHz. What is the speed of soind in steel?

A

6.2 km/s

B

5.06 km/s

C

7.23 km/s

D

7.45 km/s

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

In fundamental mode,
$l = 2 (\frac{λ}{4}) = \frac{λ}{4} \Rightarrow λ = 2 l$
Given, $l = 100 c m, v = 253 k H z$
Using v=v $λ$
$\Rightarrow v = 2.53 \times 10^{3} \times 2 \times 1000 \times 10^{- 2}$
$\Rightarrow v = 2.53 \times 10^{3} \times 2 \times 1000 \times 10^{- 2}$

|

Updated on:21/07/2023

Class 12 PHYSICS SOUND WAVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A steel rod 100 cm long is clamped at its midpoint. The fundamental frequency of longitudinal vibrtions of the rod is 3 kHz. What is the speed of the sound in the rod?
A $3 \times 10^{3} m s^{- 1}$
B $4 \times 10^{3} m s^{- 1}$
C $5 \times 10^{3} m s^{- 1}$
D $6 \times 10^{3} m s^{- 1}$
Question 2 - Select One
A steel rod of length 100 cm is clamped at the middle. The frequency of the fundamental mode for the longitudinal vibrations of the rod is
(Speed of sound in steel = 5 km $s^{- 1}$ )
A1.5 KHz
B2 KHz
C2.5 KHz
D3 KHz
Question 3 - Select One
A string is under tension sot that its length uncreased by $\frac{1}{n}$ times its original length . The ratio of fundamental frequency of longitudinal vibrations and transverse vibrations will be
A1:n
B $n^{2} : 1$
C $\sqrt{n} : 1$
Dn:1

BITSAT GUIDE-SOUND WAVES-BITSAT Archives

Home
Ask Doubt
Profile