A steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod is given to be 2.53k Hz. What is the speed of sound in steel?

Video Solution

Text Solution

Verified by Experts

Here, $l = 100 c m = 1 m, v = 2.53 k H z = 2.53 \times 10^{3} H z$
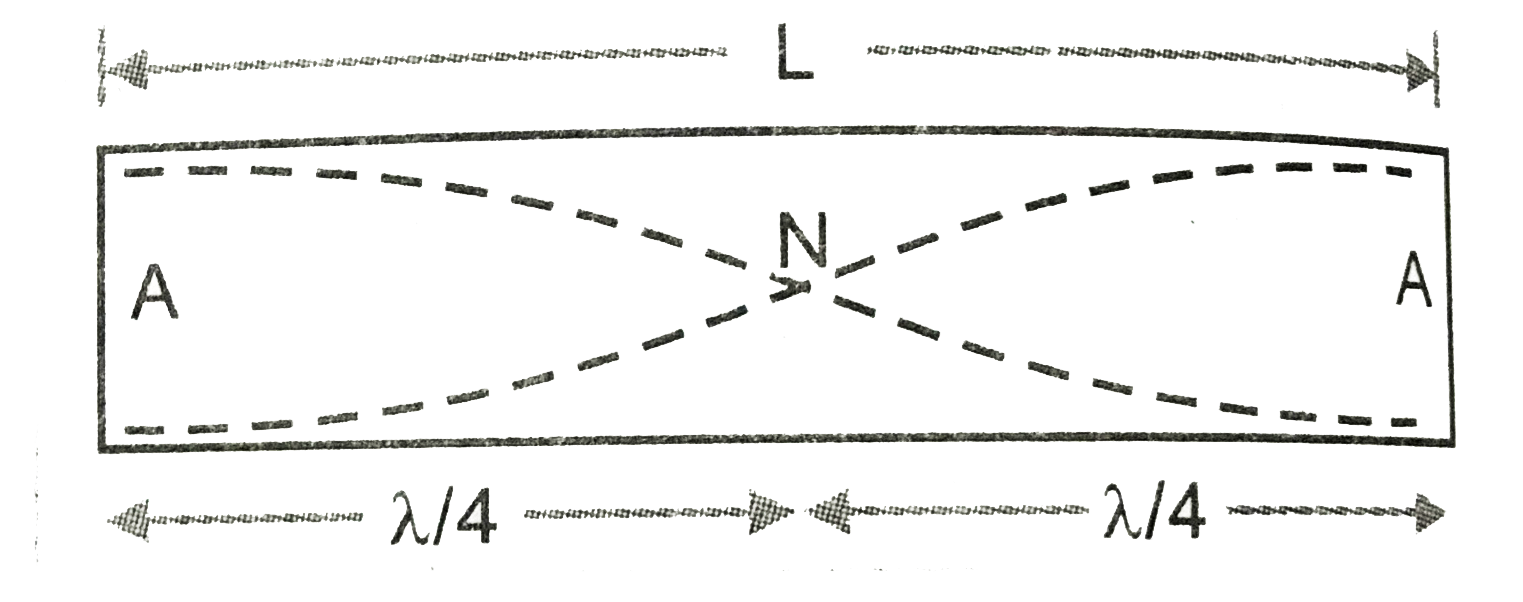
When the rod is cleampled at the middle, then in the fundamental mode of vibration of the rod, a node is formed at the middle and anitnode is formed at each end.
Therefore, as is clear from figure.
$L = \frac{λ}{4} + \frac{λ}{4} = \frac{λ}{2}$
$λ = 2 L = 2 m$
As, $υ = v λ$
$∴ υ = 2.53 \times 10^{3} \times 2 = 5.06 \times 10^{3} m s^{- 1}$

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A steel rod 100 cm long is clamped at its midpoint. The fundamental frequency of longitudinal vibrtions of the rod is 3 kHz. What is the speed of the sound in the rod?
A $3 \times 10^{3} m s^{- 1}$
B $4 \times 10^{3} m s^{- 1}$
C $5 \times 10^{3} m s^{- 1}$
D $6 \times 10^{3} m s^{- 1}$
Question 2 - Select One
A steel rod 100 cm long is clamped at its middle. The fundamental frequency of loungitudinal vibrations of the fundamental frequency of longitudinal vibrations of the rod are given to be 2.53 KHz. What is the speed of soind in steel?
A6.2 km/s
B5.06 km/s
C7.23 km/s
D7.45 km/s
Question 3 - Select One
A steel rod of length 100 cm is clamped at the middle. The frequency of the fundamental mode for the longitudinal vibrations of the rod is
(Speed of sound in steel = 5 km $s^{- 1}$ )
A1.5 KHz
B2 KHz
C2.5 KHz
D3 KHz

PRADEEP-OSCILLATIONS AND WAVES-NCERT CHAPTER

Home
Ask Doubt
Profile