(i) For the wave on a string described in question, do all theh points on the string oscillate with the same (a) frequency, (b) phase, (c) amplitude ? Explain your answers. (ii) What is the amplitude of a point 0.375m away from one end?
All the points on the string (i) have the same frequency except at the nodes (where frequency is zero) (ii) have the same phase everywhere in one loop except at the nodes.
However, the amplitude of vibration at different points is different.
From y(x,t)=0.06sin(2π3)xcos(120πt),
the amplitude at x(=0.375m)is=0.06sin(2π3)×1=0.06sin(2π3)×0.375=0.06sin(π4)=0.06√2
=0.042m
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Higher Order Thinking Skills
13 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Value Based Questions
5 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Additional Exercises
6 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
Similar Questions
The transverse displacement of a string (clamped at its two ends ) is given by y(x,t)=0.06sin(2π)3xcos120πt,
where x, y are in m and t is in s.
Do all the points on the string oscillate with theh same
(a) frequency (b) phase (c) amplitude
Explain your answer.
View SolutionA transverse harmonic wave is propagating along a taut string. Tension in the string is 50 N and its linear mass density is 0.02kgm–1 The string is driven by a 80Hz oscillator tied to one end oscillating with an amplitude of 1mm. The other end of the string is terminated so that all the wave energy is absorbed and there is no reflection
(a) Calculate the power of the oscillator.
(b) The tension in the string is quadrupled. What is new amplitude of the wave if the power of the oscillator remains same?
(c) Calculate the average energy of the wave on a 1.0m long segment of the string.
View Solution
Knowledge Check
The displacement of a vibrating string versus position along the string is shown in the figure. The periodic wave have a speed of 10.0cm/s. A and B are two points on the string.
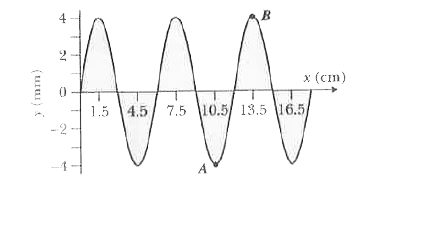
What is the amplitude of the wave?A2 mmB4 mmC12 mmD8 mm
An harmonic wave has been set up on a very long string which travels along the length of the string. The wave has a frequency of 50 Hz, amplitude 1 cm and wavelength 0.5 m. find
(a) the time taken by the wave to travel a distance of 8 m along the length of string (b) the time taken by a point on the string to travel a distance of 8 m, once the wave has reached the point and sets it into motion (c ) also. consider the above case when the amplitude gets doubled
View SolutionAdjacent antinodes of a standing wave on a string are 15.0 cm apart. A particle at an antinode oscillates in simple harmonic motion with amplitude 0.850 cm and period 0.0750 s. The string lies along the +x-axis and is fixed at x=0.
(a) find the displacement of a point on the string as a function of position and time.
(b) Find the speed of propagation of a transverse wave in the string.
(c) Find the amplitude at a point 3.0 cm to the right of an antinode.
View SolutionTwo identical sinusoidal waves, moving in same direction along a stretched string, interfere, with each other. The amplitude of each wave is 10.0mm, and the phase difference between them is 80∘. What is the amplitude of the resultant wave and the nature of interference ?
View SolutionTwo identical sinusoidal waves, moving in the same direction along a stretched string, interfere with each other. The amplitude y of each wave is 9.8 mm, and the phase difference p between them is 100∘.
(a) What is the amplitude y. of the resultant wave due to the interference, and what is the type of this interference?
(b) What phase difference, in radians and wavelengths, will give the resultant wave an amplitude of 4.9 mm?
View SolutionA wave travelling on a string at a speed of 10ms−1 causes each particle of the string to oscillate with a time period of 20 ms. (a) What is the wavelength of the wave ? (b) If the displacement of a particle is 1.5 mm at a certain instant, what will be the displacement of a particle 10 cm away from it at the same instant ?
View SolutionWhat phase difference between two identical traveling waves, moving in the same direction ulung a stretched string, results in the combined wave having an amplitude 0.852 times that of the common amplitude of the two combining waves! Express your answer in (a) degrees (b) radiants, and (c) wavelengths
View SolutionA 660 Hz tuning fork sets up vibration in a string clamped at both ends. The wave speed for a transverse wave on this string is 1220ms−1 and the string vibrates in three loops. (a) Find the length of the string. (b) If the maximum amplitude of a particle is 0.5 cm, write a suitable equation describing the motion.
View Solution
