An AC voltage e=e0sin50t−e0cos100πt is connected in series with a resistor and capacitor. The steady state current through circuit is found to be I=I0sing(50πt+ϕ)+I0'cos(100πt+ϕ2)
Then, the ratio of I0I0' is
greater than 1
equal to 1
less than 1
None of these
( C ) l0=E0√R2+XC=2=E0√R2+(150C)2
Similarly ,
l'0=E0√R2+(1100C)2 Hence ,l_(0)ltl_(0)
Topper's Solved these Questions
Similar Questions
An AC source producing emf
ε=ε0[cos(100πs−1)t+cos(500πs−1)t]
is connected in series with a capacitor and a resistor. The steady-state current in the circuit is found to be
I=i1cos[(100πs−1t+φ1]+i2cos[(500πs−1)t+ϕ2].
View SolutionAnalternating voltage E=E0sinωt is applied to a circuit containıng a resistor R connected in series with a black box. The current in the circuit is found to be =I0sin(ωt+π/4).
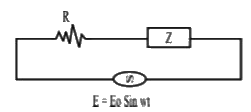
State whether the element in the black box is a capacitor or inductor.
View Solution
Knowledge Check
An AC source producing e.m.f V=V0(sinωt+sin3ωt) is connected in series with a capacitor and a resistor. The current in the circuit is found to be i=i1sin(ωt+ϕ1)+i2sin(3ωt+ϕ2) then comment
Ai1>i2Bi1=i2Ci1<i2Dany of the above may be trueAn AC source producing emf V=V0 "["sin omega t+sin 2omegat"]" is connected in series with a capacitor and a resistor. The current found in the circuit is
Ai1−i2Bi1<i2Ci1>i2Di1 may be less than, equal to or greater than i2Voltage and current is an AC circuit are given by V=sin(100πt−π6) and I=4sin(100πt+π6)
AVoltage leads the current by 30∘BCurrent leads the voltage by 30∘CCurrent leads the voltage by 60∘DVoltage leads the current by 60∘
Analternating voltage E=E0sinωt is applied to a circuit containıng a resistor R connected in series with a black box. The current in the circuit is found to be =I0sin(ωt+π/4).
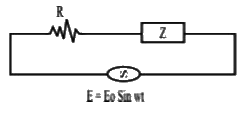
Draw the corresponding phasor diagram and find the impedance in tems of R.
View SolutionA 31.4Ω resistor and 0.1H inductor are connected in series to a 200V, 50Hz ac source. Calculate
(i) the current in the circuit
View SolutionAn ac source producing V=V0sinωt+V0sin2ωt is connected in series with a box containing either capacitor or inductor and resistance. The current found in the circuit is I=I1sin(ωt+ϕ1)+I2sin(2ωt+ϕ2) . Here, ϕ1 and ϕ2 may be positive or negative.
View SolutionAn alternating emf, e=300 sin100πt volt, is applied to a pure resistance of 100 Ω. The rms current through the circuit is
View SolutionThe emf and the current in a circuit are – E=12sin(100πt),i=4sin(100πt+π/3) then–
View Solution
