Analternating voltage E=E0sinωt is applied to a circuit containıng a resistor R connected in series with a black box. The current in the circuit is found to be =I0sin(ωt+π/4).
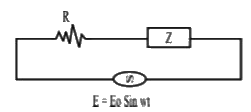
State whether the element in the black box is a capacitor or inductor.
As the current leads the voltage by ,π4 the element used in black box is a ‘capacitor’.
Topper's Solved these Questions
- SAMPLE QUESTION PAPER 2019BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SAMPLE QUESTION PAPER 2019EXERCISE - Section C
19 Videos
- SAMPLE QUESTION PAPER 2019BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SAMPLE QUESTION PAPER 2019EXERCISE - Section C
19 Videos
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - NUMERICALS
49 Videos
- UNIT–III & UNIT–IV MAGNETIC EFFECTS OF CURRENT AND MAGNETISM & E.M.I. AND ALTERNATING CURRENTBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - UNIT–III & UNIT–IV MAGNETIC EFFECTS OF CURRENT AND MAGNETISM & E.M.I. AND ALTERNATING CURRENTEXERCISE - (NUMERICALS)
57 Videos
Similar Questions
Analternating voltage E=E0sinωt is applied to a circuit containıng a resistor R connected in series with a black box. The current in the circuit is found to be =I0sin(ωt+π/4).
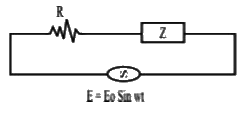
Draw the corresponding phasor diagram and find the impedance in tems of R.
View SolutionAn voltage, E=E0sinωt is applied acorss an inductor L. Obtain an expression for the current.
View Solution
Knowledge Check
If an alternating voltage V=V_0 sin omegat is applied across an inductance I, the current through the inductance will be
AI=I0sinωtBI=I0sin(ωt+π/2)CI=I0sin(ωt+π/2)DI=I0sin(ωt+π)If an alternating voltage V=V_0 sin omegat is applied across an inductance I, the current through the inductance will be
AI=I0sinωtBI=I0sin(ωt+π/2)CI=I0sin(ωt+π/2)DI=I0sin(ωt+π)A small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
ACurrent l(t) leads voltage V(t) by 180∘BCurrent l(t) lags voltage V(t) by 90∘COver a full cycle the capacitor C does not consume any energy from the voltage sourceDCurrent l(t) is in phase with voltage V(t)
An alternating voltage V=V0sinωt is applied across a circuit. As a result, a current I=I0sin(ωt–p2) flows in it. The power consumed per cycle is
View SolutionAn AC source producing emf V=V0 "["sin omega t+sin 2omegat"]" is connected in series with a capacitor and a resistor. The current found in the circuit is
View SolutionAn AC source producing e.m.f V=V0(sinωt+sin3ωt) is connected in series with a capacitor and a resistor. The current in the circuit is found to be i=i1sin(ωt+ϕ1)+i2sin(3ωt+ϕ2) then comment
View SolutionAn alternating voltage E=E0sinωt , is applied across a coil of inductor L. The current flowing through the circuit at any instant is
View SolutionA small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
View Solution
