An amusement park ride consist of a large verticle cylinder that spins about its axis first fast enough that any person inside is held up againest the wall when the is μs and the radius of the cylider is R

a. Shown that maximum period of revolation neccessary to keep the person from falling is T=(4π2μs/g)1/2
b. Obtain a numerical value for taking R=4.00m and μs=0.400 . How many revolations per minute does the cylinder make?
c.If the rate of revolation of the cylinder is make to be some what larger what happens to the magnitude of each one of the forces acting on the person ? What happens to the motion of the person ?
d.If instead the cylinder rate revolation is made to be somewhat smaller what happens to the magnitude happens to the motion of the person ?
The correct Answer is:B, C
Step by step video, text & image solution for An amusement park ride consist of a large verticle cylinder that spins about its axis first fast enough that any person inside is held up againest the wall when the is mu_(s) and the radius of the cylider is R a. Shown that maximum period of revolation neccessary to keep the person from falling is T = (4 pi^(2) mu_(s) //g)^(1//2) b. Obtain a numerical value for taking R = 4.00m and mu_(s) = 0.400 . How many revolations per minute does the cylinder make? c.If the rate of revolation of the cylinder is make to be some what larger what happens to the magnitude of each one of the forces acting on the person ? What happens to the motion of the person ? d.If instead the cylinder rate revolation is made to be somewhat smaller what happens to the magnitude happens to the motion of the person ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved
1 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - MCQ
158 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical
63 Videos
Similar Questions
A solid cylinder of mass 20kg rotates about its axis with angular velocity of 100 radian s−1. The radius of the cylinder is 0.25m. The magnitude of the angular momentum of the cylinder about its axis of rotation is
View SolutionLet the period of revolution of a planet at a distance R from a star be T. Prove that if it was at a distance of 2R from the star, its period of revolation will be √8T.
View Solution
Knowledge Check
An amusement park ride called "The spinning Terror" is a large vertical drum which spins so fast that everyone stays pinned against the wall when the floor drops away the minimum
Aangular velocity is ωmin=√gμR for everyone to stay inside.Blinear velocity is vmin=√gμR for everyone to stay inside.Cangular velocity is ωmin=√gRμ for everyone to stay inside.Dlinear velocity is vmin=√gRμ for everyone to stay inside.A current of I ampere flows along an infinitely long straight thin walled hollow metallic cylinder of radius r. The magnetic field at any point inside the cylinder at a distance x from the axis of the cylinder is
A∞Bμ0I2πrCμ0I2πxDzeroA solid cylinder of mass 20kg rotates about its axis with angular velocity of 100 radian s−1. The radius of the cylinder is 0.25m. The magnitude of the angular momentum of the cylinder about its axis of rotation is
A62.6 J sB70.4 J sC79.6 J sD60.5 J s
A person stands in contact against the inner wall of a rotor of radius r. The coefficient of friction between the wall and the clothing is μ and the rotor is rotating about vertical axis. The minimum angular speed of the rotor so that the person does not slip downward is
View Solution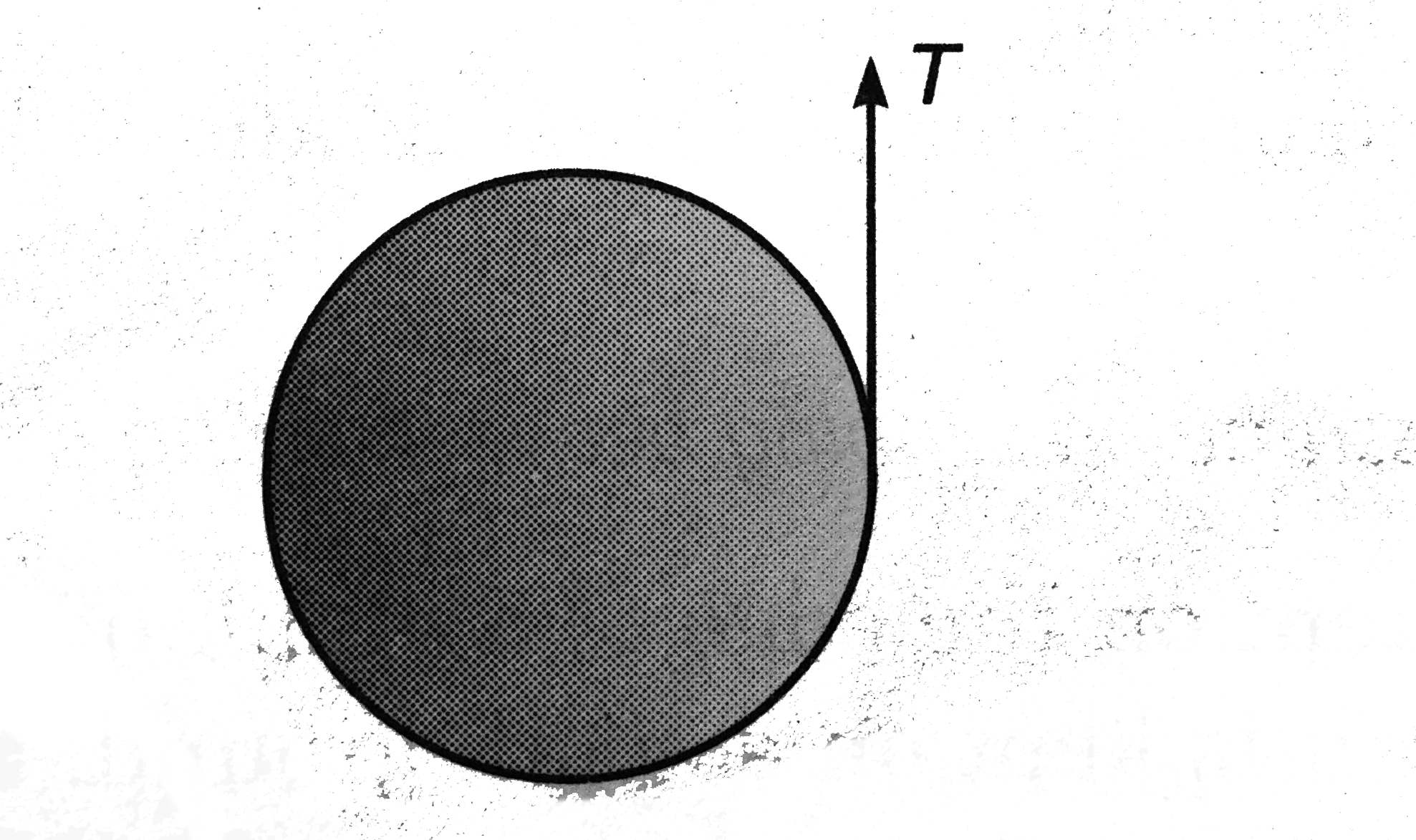
A uniform cylider of mass M and radius R has a string wrapped around it. The string is held fixed and the cylinder falls vertically, as in figure.
(a). Show that the acceleration of the cylinder is downward with magnitude a=2g3
(b). Find the tension in the string.
View SolutionA uniform cylinder of radius R is spinned about it axis to the angular velocity ω0 and then placed into a corner,. The coeficient of friction between the corner walls and the cylinder is μk How many turns will the cylinder accomplish before it stops?

View SolutionA cylinder of radius R full of liquid of density p is rotated about its axis at w rad/s. The increase in pressure at the centre of the cylinder will be
View SolutionA solid cylinder is rolling without slipping on a plane having inclination θ and the coefficient of static friction μs. The relation between θ and μs is
View Solution
