Three rods of equal length of same material are joined to form an equivalent triangle ABC as shown figure. Area of cross-section of rod AB is S of rod BC is 2S and that of AC is S , then
_E01_150_Q01.png)
Column-IColumn-II(A)Temperature of junctionB(p)Greater than50∘C(B)Heat current inAB(q)Less than50∘C(C)Heat current in BC(r)Is equal to current in BC(s)Is 23times heat current in AC(t)None
The correct Answer is:A, B, C
Thermal resistance α1Area
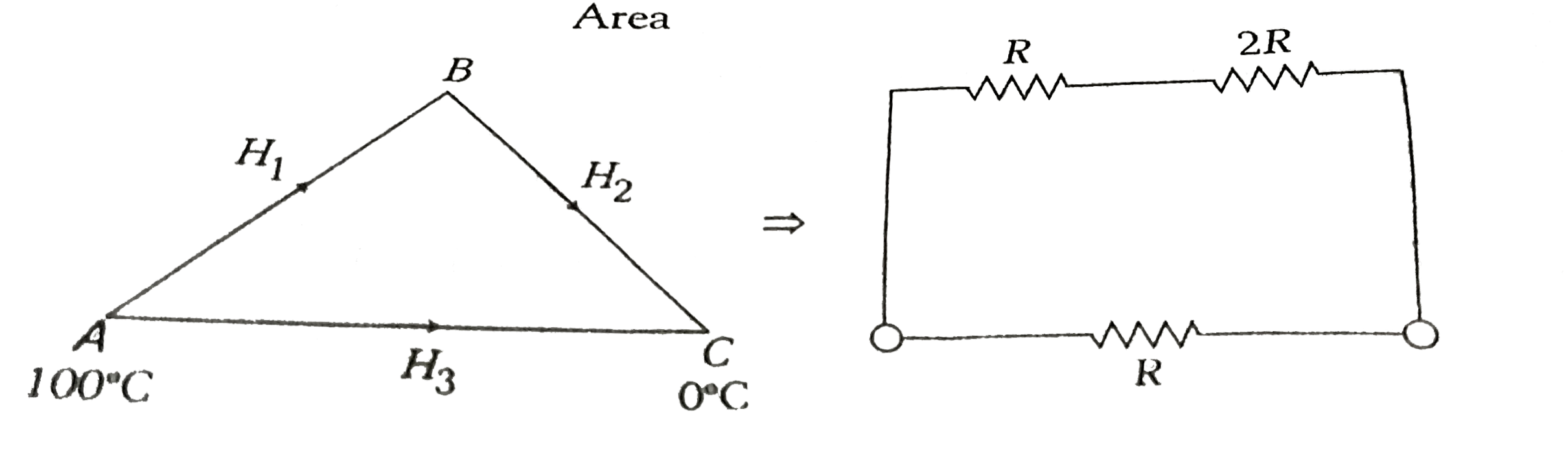
So let, RBC = R
Then RAB+RAC = 2R
H1=H2
100−θBR=θB−02R
∴ θB=66.7∘C
RABC-3R and RAC=R
H1=H2=H33
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Assertion and reason
17 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- CENTRE OF MASSBOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
Similar Questions
Three rods of equal length of same material are joined to form an equilateral triangle ABC as shown in figure. Area of cross-section of rod AB is S, of rod BC is 2S and that of AC is S. Then match the following.

View SolutionColumn IColumn II(a)Electric Generator(p)Electric to Mechanical(b)Electric Motor(q)Electric to Heat(c)Burning(r)Mechanical to Electric(d)Hair dryer(s)Chemical to Heat
View Solution
Knowledge Check
Three rods of equal of length are joined to from an equilateral triangle ABC. D is the midpoint of AB. The coefficient of linear expansion is α1 for AB and α2 for AC and BC . If the distance DC remains constant for small changes in temperature,
 Aα1=α2Bα1=2α2Cα1=4α2Dα1=1/2α2
Aα1=α2Bα1=2α2Cα1=4α2Dα1=1/2α2Three rods A,B and C of the same length and cross- sectional area are joined in series as shown. The temperature at the junction of A and B, in equilibriu, is
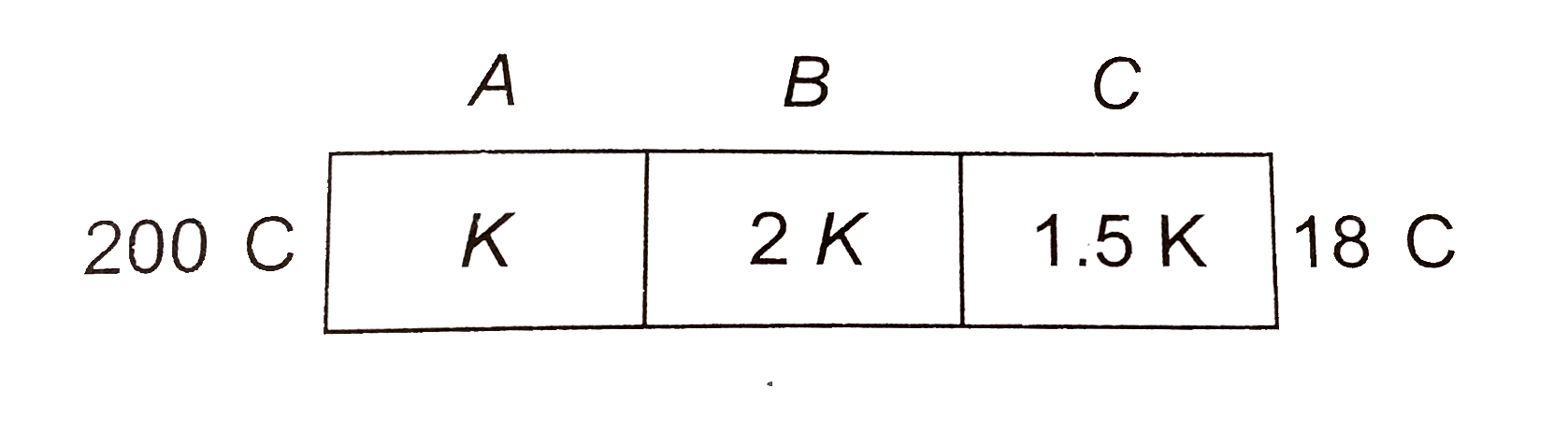 A74∘CB116∘CC156∘CD148∘C
A74∘CB116∘CC156∘CD148∘CFour rods of equal length L are joined by four pins A,B,C & D as shown in the figure. Rods are free to rotated about pins. Pin A is given velocity v0 and pin C is given 3v0 as shown
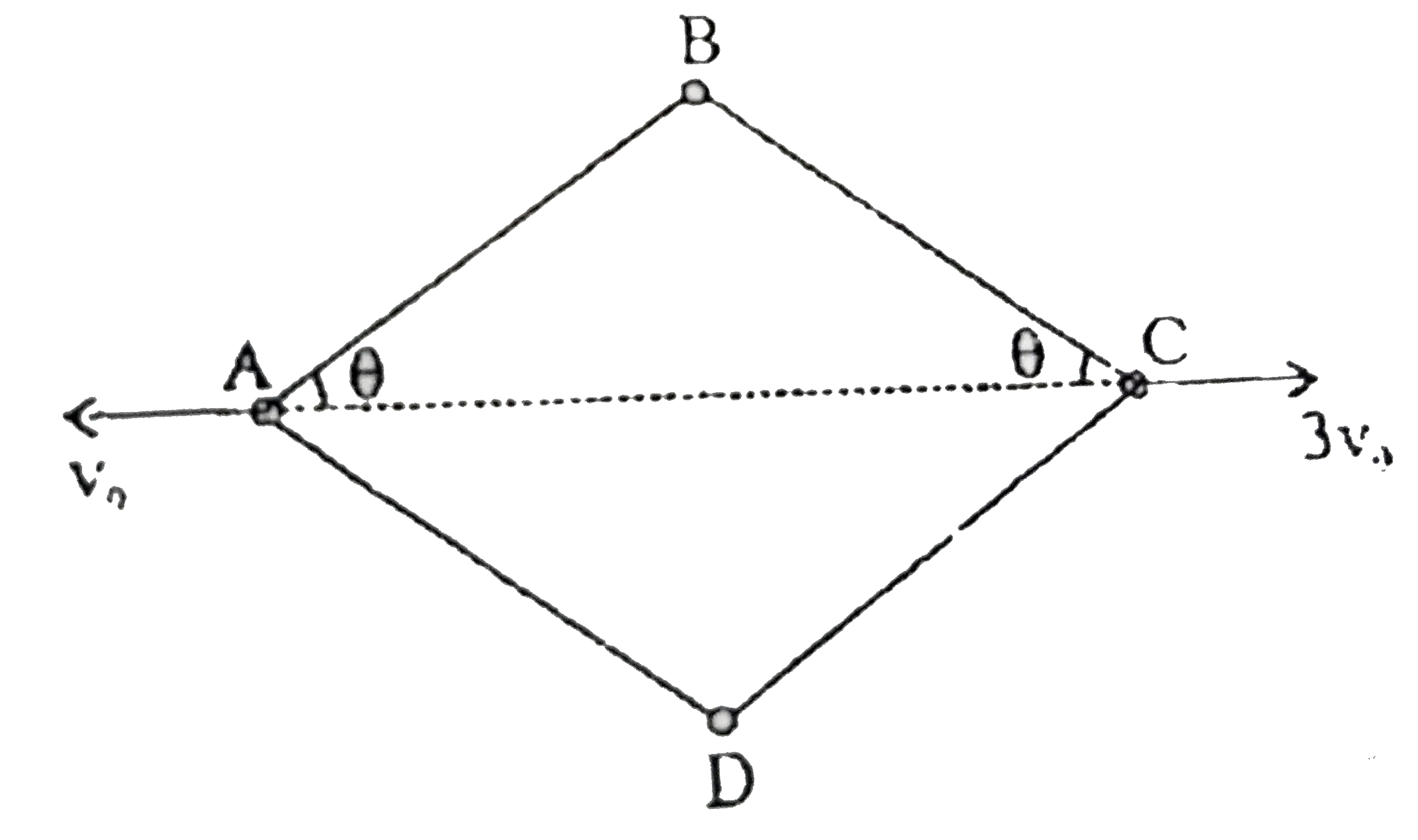
The angular velocity of rod BC isA2v0LB2v0LsinθC2v0LsinθD2v0Lcosθ
Four rods of material X and three rods of material Y are connected as shown in figure. All the rods are of identical lengths and cross-sectional area. Given thermal resistance of rod of material X,Rx=R and thermal conductivities of materials are related by relation KY=2KX.
_E01_157_Q01.png)
Column-IColumn-II(A)Thermal resistance between B and E(p)50013.∘C(B)Thermal resistance between A and F(q)70013.∘C(C)Temperature of junction B(r)2R3(D)Temperature of junction D(s)13R6
View SolutionCurrent I is following through a wire of non-uniform cross-section as shown. Match the following columns.
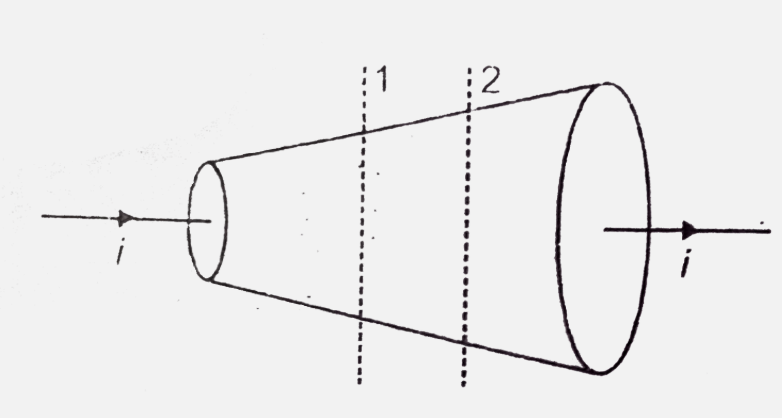
Column IColumn II(A)Current density(p)More at section 1 than 2(B)Electric field(q)More at section 2 than 1(C)Resistance per unit length(r)Same at both section 1 and 2 (D)Potential difference per unit length(s)Data insufficient
View SolutionMatch the quantity of Column I with the quantity of Column II
Column IColumn II(A)Glycine(p)Has S-S linkage(B)Arginine(q)Optically active(C)Glutamic acid(r)Has pH less than 7(D)Cystine(s)Has pH greater 7
View SolutionThree rods of equal length, area of cross section and thermal conductivity are connected as shown in the figure.

There is no heat loss through lateral surface of the rods and temperature of ends are TA=100∘C,TB=70∘C and TC=50∘C. Find the temperature of junction.
View SolutionThree liquids A,B and C having same specific heat and mass m , 2m and 3 m have temperature 20∘C,40∘C and 60∘C respectively. Temperature of the mixture when:
Column-IColumn-II(A)A and B are mixed(p)35∘C(B)A and C are mixed(q)52∘(C)B and C are mixed(r)50∘(D)A,B and C all three are mixed(s)45∘(t)None
View Solution
