A solid disk is rolling without slipping on a level surface at a constant speed of 2.00m/s. How far can it roll up a 30∘ ramp before it stops? (take g=9.8m/s2)
Video Solution
Text Solution
The moment of inertia of the sphere about its axis of rotation is I=25mr2. Suppose it rises to height h before stopping. Using the conservation of energy, we get
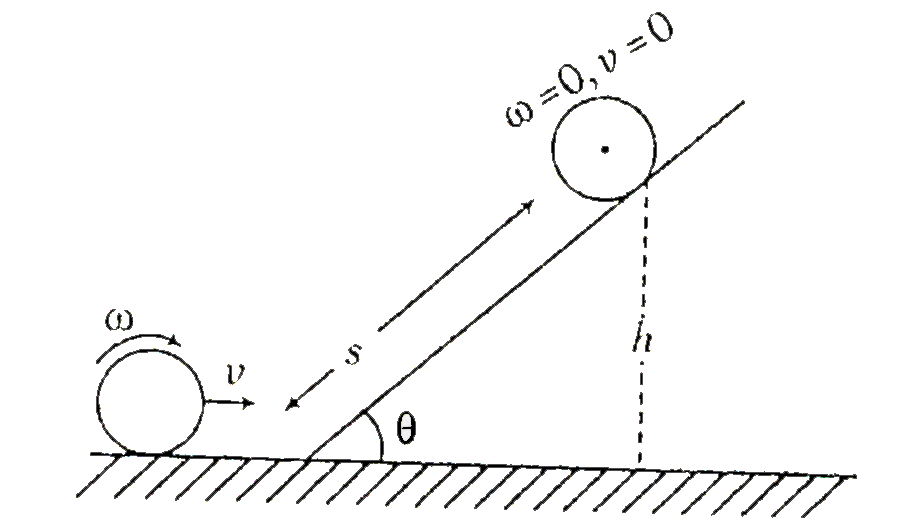
mgh=12mv2+12Iω2=12mv2+12(25mr2)ω2
=12mv2+15mv2=710mv2orh=7v210g
∴ The distance rolled up on the ramp is
s=hsinθ=7v210gsinθ=7(2 ms−1)210(9.8ms−2)×1/2=47metre≅57cm
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.120videos
ROTATION
- BOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.220videos
ROTATION
- BOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.15videos
RAY OPTICS
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions2videos
ROTATIONAL MECHANICS
Similar Questions
Knowledge Check
- Question 1 - Select One
A solid sphere is rolling without slipping on a level surface dat a constant speed of 2.0ms−1 How far can it roll up a 30∘ ramp before it stops ?
A56 cmB26 cmC53 cmD84 cm - Question 2 - Select One
A ball is thrown up with a speed of 15 m/s . How high wiil it go before it begins to fall ? (g=9.8m/s2
A11.4 mB15 mC4 mDNone - Question 3 - Select One
A uniform sphere of mass 500g rolls without slipping on a plane surface so that its centre moves at a speed of 0.02m/s.
The total kinetic energy of rolling sphere would be (in J)A1.4×10−4JB0.75×10−3JC5.75×10−3JD4.9×10−5J
A stone is thrown vertically upwards with a speed of 20 m/s. How high will it go before it begins to fall? (g=9.8m/s2)
View SolutionA unifrom sphere of mass 500 g rolls without slipping on a plants horizontal surface with its center moving at a speed of 5.00cm/s .It kinetic energy is :
View SolutionA symmetrical body of mass M and radius R is rolling without slipping on a horizontal surface with linear speed v. Then its angular speed is
View SolutionA solid sphere rolls down without slipping on an inclined plane at angle 60∘ over a distance of 5 m. The acceleration (in ms−2) is
View SolutionA solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
View Solution

