A solid sphere is rolling down an inclined plane without slipping of height 20 m. Calculate the maximum velocity with which it will reach the bottom of the plane (g=10m/s2)
When the sphere rolls down, its potential energy changes to KE of rotation. Therefore, KE=PE
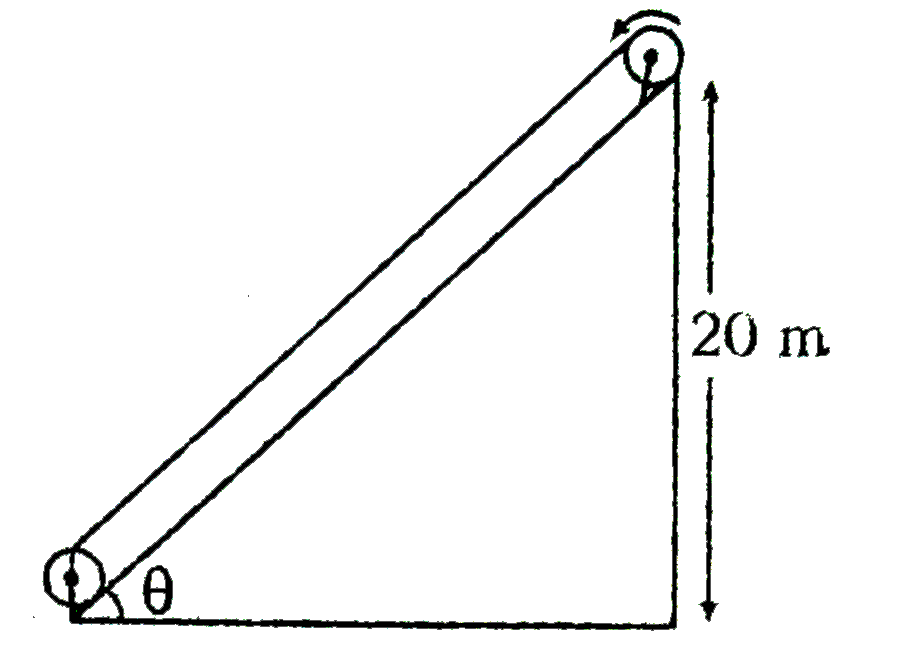
12mv2(1+K2R2)=mgh
⇒v=√2gh(1+K2/R2)
Moment of inertia of solid sphere =25MR2
∴K2=25R2
Hence, v=
⎷2gh(1+25)=√2gh×57=√2×10×20×57
=√285.714=16.90m/s.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.1
20 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.2
20 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.
15 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
A solid cylinder, of mass 2 kg and radius 0.1 m, rolls down an inclined plane of height 3m. Calculate its rotational energy when it reaches the foot of the plane.
View SolutionA uniform ring rolls down an inclined plane without slipping. If it reaches the bottom of a speed of 2m/s, then calculate the height of the inclined plane (use g=10m/s2)
View Solution
Knowledge Check
A solid cylinder is rolling down the inclined plane without slipping. Which of the following is correct?
AThe friction force is dissipativeBThe friction force is necessarity changingCThe friction force will aid rotation but hinder translationDThe friction force is increased if θ is reducedA sphere rolls down an inclined plane through a height h. Its velocity at the bottom would be
A√2ghB√710ghC√107ghD(√107)ghA solid cylinder is rolling down the inclined plane without slipping. Which of the following isare correct?
AThe friction force is dissipativeBThe friction force is necessarily changingCThe friction force will aid rotation but hinder translationDThe friction force is reduced, if ~theta~ reduced
A solid sphere of mass M and radius R, rolling down a smooth inclined plane, without slipping, reaches the bottom with a velocity v. What is the height of the inclined plane in terms of the velocity v ?
View SolutionA ring, a solid cylinder and sphere are rolled down on an inclined plane without slipping. Velocity of centre of mass is
View SolutionA solid cylinder rolls down from an inclined plane of height h. What is the velocity of the cylinder when it reaches at the bottom of the plane ?
View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h. The angular velocity of the cylinder when it reaches the bottom of the plane will be :
View SolutionA solid sphere of mass 1 kg, redius 10 cm rolls down an inclined plane of height 7m. The velocity of its centre as it reaches the ground level is
View Solution