A solid flywheel of 20 kg mass and 120 mm radius revolves at 600revmin−1. With what force must a brake lining be pressed against it for the flywheel to stop in 3s, if the coefficient of friction is 0.1 ?
Given, revolutions per minute, n0=600rev min−1
=60060rev s−1
Revolutions per second, n0=10rev s−1
So, initial angular velocity, ω0=2πn0=(2π)(10)=20πrad s−1
Let α be the constant angular retardation, then applying
ω=ω0=αt
or 0=(20π)−3(α)
or α=203πrad s−2
Further, α=τI
Here, torque τ=μNR (R=radius)
or τ=μFR (F=applied force)
=N=FandI=12mR2
From the above equations,
203π=μFR12mR2=2μFmR
or Force, F=10πmR3μ
Substituting the values, we have
F=10×22×20×0.123×7×0.1
or F=2.51.43N.
Topper's Solved these Questions
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:Check point 9.1
Explore 20 Videos
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:Check point 9.2
Explore 20 Videos
- RAY OPTICSBook:DC PANDEYChapter:RAY OPTICSExercise:Integer type q.
Explore 15 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
Similar Questions
A solid flywheel of 20 kg mass and 120 mm radius revolves at 600 r.p.m. With what force must a brake lining be pressed against it for the flywheel to stop in 3 s, if the coefficient of friction is 0.1?
View SolutionA scooter weighs 120 kg f. Brakes are applied so that wheels stop rolling and start skidding. Find the force of friction if the coefficient of friction is 0.4.
View Solution
Knowledge Check
A solid flywheel of mass M and radius r revolves with an angular velocity m. With what force must a brake lining be pressed against it for the flywheel to stop in t seconds, if μ is the coefficient of friction?
AMrω2μtBrω2μMtCMω2μrtDMωt2μrA marble block of mass 2 kg lying on ice when given a velocity of 6m/s is stopped by friction in 10s. Then the coefficient of friction is
A0.02B0.03C0.06D0.01A block of mass 1 kg is held at rest against a rough vertical surface by pushing by a force F horizontally. The coefficient of friction is 0.5. When
 AF = 40 N, friction on the block is 20 N.BF = 30 N, friction on the block is 10 N.CC = 20 N, friction on the block is 10 N.DMinimum value of force F to keep block at rest is 20 N.
AF = 40 N, friction on the block is 20 N.BF = 30 N, friction on the block is 10 N.CC = 20 N, friction on the block is 10 N.DMinimum value of force F to keep block at rest is 20 N.
A flywheel of mass 25 kg has a radius of 0.2 m. What force should be applied tangentially to the rim of the flywheel so that it acquires an angular acceleration of 2rad s−2 ?
View SolutionGiven in figure are two blocks A and B of weight 20N and 100N, respectively. These are being pressed against a wall by a force F as shown. If the coefficient of friction between the blocks is 0.1 and between block B and the wall is 0.15, the frictional force applied by the wall on block B is:

View SolutionA rectangular block of mass 6 kg is to be held against a rough vertical wall by appplying a force perpendicular to the wall. What is the minimum force to be applied, if the coefficient of friction is 0.42?
View SolutionA board of mass m = 1 kg lies on a table and a weight of M = 2 kg on the board. What minimum force F must be applied on the board in order to pull it out from under the road ? The coefficient of friction between board and table is μ2=0.5 : (Take g=10m/s2)
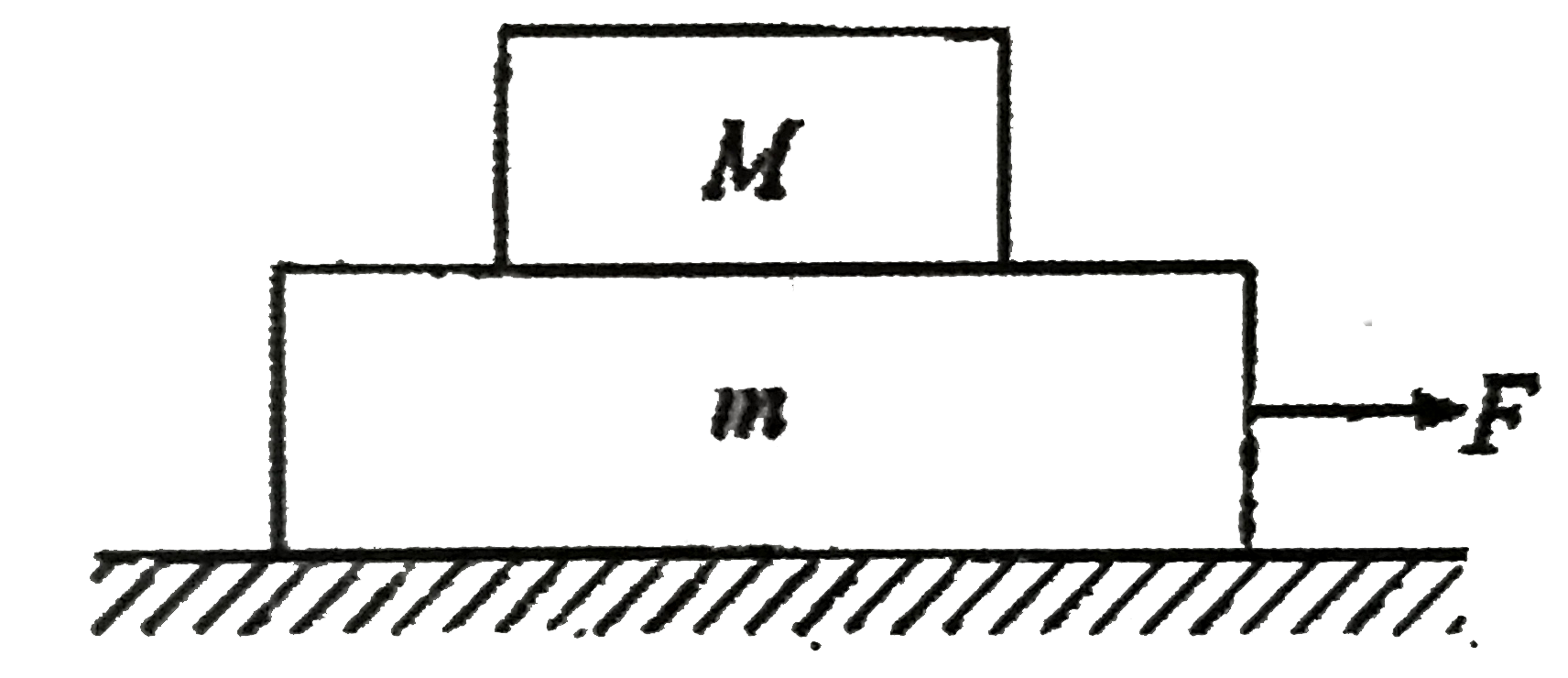
View SolutionA marble block of mass 2 kg lying on ice when given a velocity of 6ms−1 is stopped by friction in 10 s. Then the coefficient of friction is (g=10ms−2)
View Solution

