Which of the following points lies the greatest distance from the origin in the xy-plane?
The correct Answer is:A
To determine which of the given points lies the greatest distance from the origin in the xy-plane, we will use the distance formula. The distance d from a point (x,y) to the origin (0,0) is given by:
d=√(x−0)2+(y−0)2=√x2+y2
Now, we will calculate the distance for each point provided.
Step 1: Calculate the distance for the first point (−32,−32)
d1=√(−32)2+(−32)2
=√94+94=√184=√92=3√2
Step 2: Calculate the distance for the second point (−1,−1)
d2=√(−1)2+(−1)2
=√1+1=√2
Step 3: Calculate the distance for the third point (−12,0)
d3=√(−12)2+02
=√14=12
Step 4: Calculate the distance for the fourth point (0,1)
d4=√02+12
=√1=1
Step 5: Compare the distances
Now we have the distances:
- d1=3√2
- d2=√2
- d3=12
- d4=1
To compare these distances, we can convert them to a common format or approximate their values:
- d1≈2.12
- d2≈1.41
- d3=0.5
- d4=1
Conclusion
The greatest distance from the origin is d1=3√2. Therefore, the point that lies the greatest distance from the origin is:
Answer: (−32,−32)
---
=√94+94=√184=√92=3√2
=√1+1=√2
=√14=12
=√1=1
- d1=3√2
- d2=√2
- d3=12
- d4=1
- d1≈2.12
- d2≈1.41
- d3=0.5
- d4=1
Topper's Solved these Questions
- FUNCTIONS AND GRAPHSBook:PRINCETONChapter:FUNCTIONS AND GRAPHSExercise:Functions and Graphs Drill 1: No Calculator Section
Explore 5 Videos
- FUNCTIONS AND GRAPHSBook:PRINCETONChapter:FUNCTIONS AND GRAPHSExercise:Functions and Graphs Drill 2: Calculator-Permitted Section
Explore 4 Videos
- FUN WITH FUNDAMENTALSBook:PRINCETONChapter:FUN WITH FUNDAMENTALSExercise:Fundamental Drill 2: Calculator- Permitted Section
Explore 6 Videos
- GEOMETRYBook:PRINCETONChapter:GEOMETRYExercise:Geometry Drill 1: No calculator Section
Explore 4 Videos
Similar Questions
Knowledge Check
Which of the following equations describes the set of all point (x, y) in the coordinate plane that are a distance of √3 from the point (2,−5) ?
A(x−2)2+(y−5)2=3B(x−2)2+(y+5)2=3C(x+2)2+(y+5)2=3D(x+2)2−(y−5)2=3
Find the locus of point whose distance from the origin is 5.
View SolutionFind the distance of the point (2, 3, 5) from the xy-plane.
View SolutionFind the locus of a point which moves such that its distance from the origin is three times its distance from x-axis.
View SolutionFind the distance of point P(x,y) from the origin
View SolutionIn the following four situations charged particles are equal distance from the origin. Arrange them the magnitude of the net electric field at origin greatest first
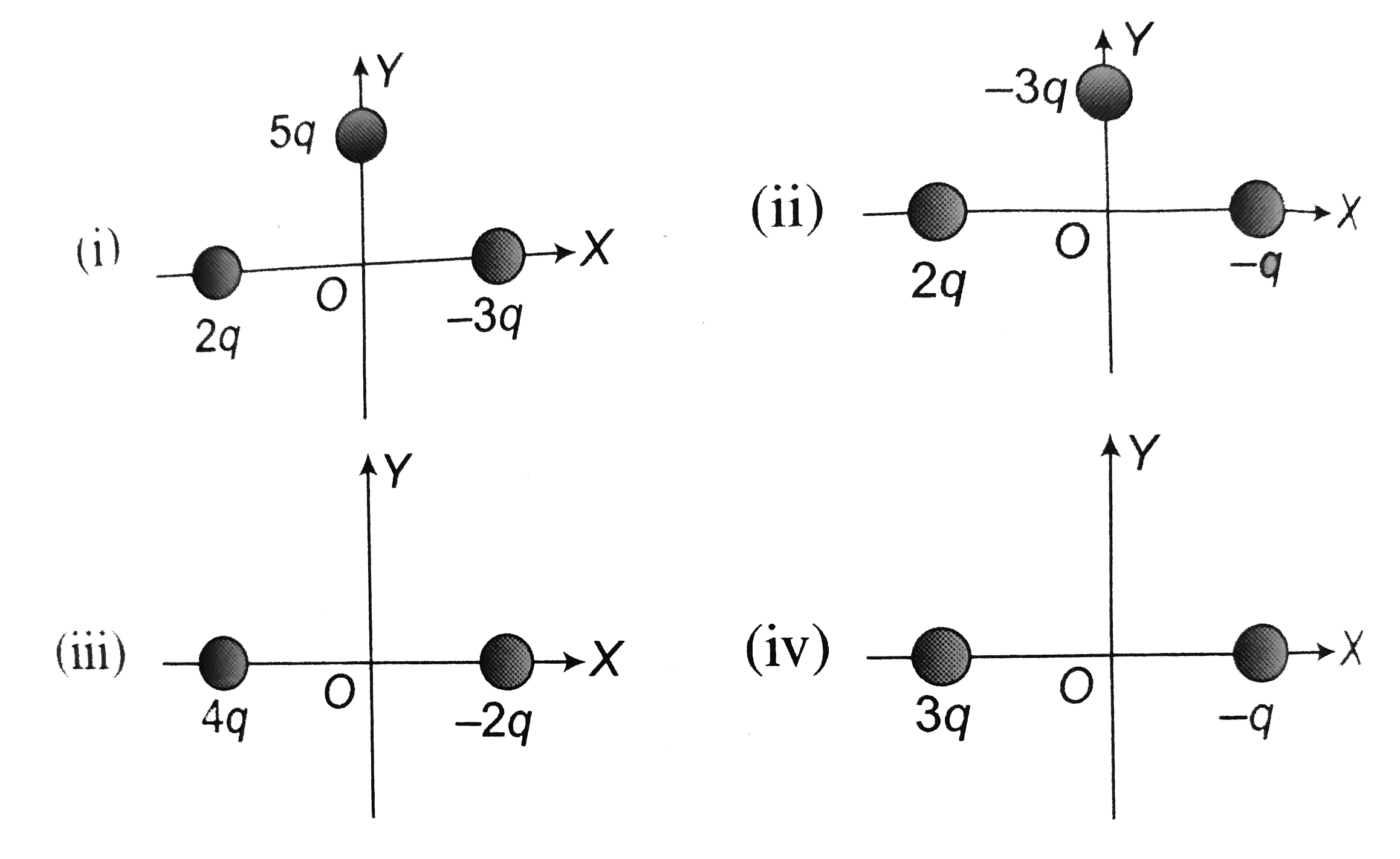
View SolutionFind the distance from the origin to each of the point:
(2,2,3)
View Solution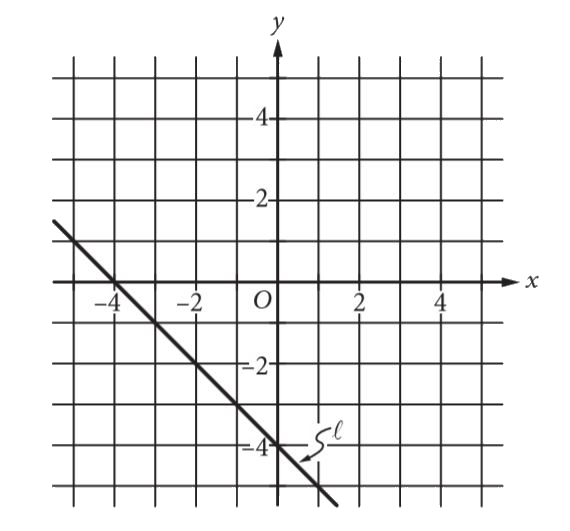
Which of the following is an equation of line in the xy -plane above?
View Solution

