x(dx+10)=−3
The equation above, where d is a constant, has no real solutions. The value of d could be which of the following?
A
−12
B
4
C
8
D
10
Video Solution
Text Solution
The correct Answer is:D
Get the equation x(dx+10)=−3into the form ax2+bx+c=0. Multiply out the left side of the equation x(dx+10)=−3 to get dx2+10x=−3. Add 3 to both sides to yield dx2+10x+3=0.
When a,b, and c are all real, the equation ax2+bx+c=0 (when a≠0) does not have real solutions only if the discriminat, which is b2−4ac, is negative. in the equation dx2+10x+3=0,a=d,b=10andc=3. The discriminant, that is, b2−4ac, is negative. In the equation is 102−4(d)(3)−100−12d.
Since you're looking for a negative discriminant, that is,b2−4ac<0, you need 100−12d<0. Solve the inequality 100−12d<0 for d:
100−12d<0
100<12d
10012<d
253<d
813<d
Among the answer choices, only 10 is greater than 813, so (D) is correct.
|
Topper's Solved these Questions
- QUADRATICSBOOK - KAPLANCHAPTER - QUADRATICSEXERCISE - SOLVING QUADRATICS BY FACTORING
1 Video
- QUADRATICSBOOK - KAPLANCHAPTER - QUADRATICSEXERCISE - CLASSIC QUADRATICS
1 Video
- QUADRATICSBOOK - KAPLANCHAPTER - QUADRATICSEXERCISE - SYSTEMS OF QUADRATIC AND LINEAR EQUATIONS
1 Video
- PAIRED PASSAGES AND PRIMARY SOURCE PASSAGES BOOK - KAPLANCHAPTER - PAIRED PASSAGES AND PRIMARY SOURCE PASSAGES EXERCISE - HOW MUCH HAVE YOU LEARNED
11 Videos
- SAT MATH: TIMING ANS SECTION MANAGEMENT STRATEGIESBOOK - KAPLANCHAPTER - SAT MATH: TIMING ANS SECTION MANAGEMENT STRATEGIESEXERCISE - TRY ON YOU OWN
5 Videos
Similar Questions
Knowledge Check
2x2−4x=t
In the equation above, t is a constant. If the equation has no real solutions, which of the following could be the value of t ?A−3B−1C1D3ax3+bx2+cx+d=0
In the equation above, a, b, c, and d are constants. If the equation has roots −1, −3, and 5, which of the following is a factor of ax3+bx2+cx+d ?Ax-1Bx+1Cx − 3Dx+5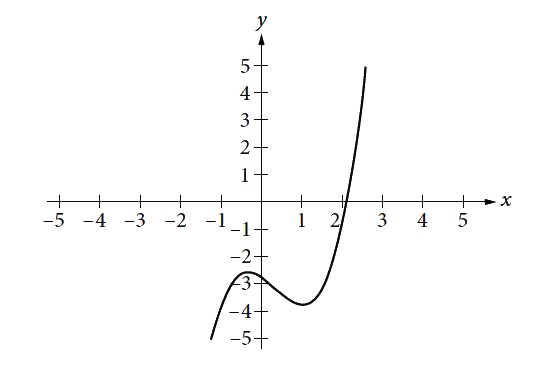
The function f(x)=x3−x2−x−114 s graphed in the xy-plane above. If k is a constant such that the equation f(x)=k has three real solutions, which of the following could be the value of k ?A2B0C−2D−3
a(x+b)=4x+10
In the equation above , a and b are constants. If the equation has infinitely many solutions for x , what is the value of b ?
View SolutionIf the system of linear equations above has o solution, and a is a constant, then what is the value of a ?
View SolutionIn the equation above, k is a constant. For which of the following values f k does the equation have at least one re3al solution ?
View Solution4x2−9=(px+t)(px−t)
In the equation above, p and t are constants. Which of the following could be the value of p ?
View Solution−3x + y = 6
ax + 2y = 4
In the system of equations above, a is a constant. For which of the following values of a does the system have no solution?
View Solution

