r(x)=3x−7
t(x)=3x+r(x)
The function r and t are defined above. What is the value of t(2) ?
−3
−1
0
5
The correct Answer is:D
To solve the problem, we need to find the value of t(2) using the given functions r(x) and t(x).
1. Identify the functions:
- We have r(x)=3x−7
- We also have t(x)=3x+r(x)
2. Substitute r(x) into t(x):
- To find t(x), we substitute r(x) into the equation for t(x):
t(x)=3x+r(x)=3x+(3x−7)
3. Simplify t(x):
- Combine like terms:
t(x)=3x+3x−7=6x−7
4. Now, find t(2):
- Substitute x=2 into the simplified function t(x):
t(2)=6(2)−7
5. Calculate the value:
- Perform the multiplication and subtraction:
t(2)=12−7=5
Thus, the value of t(2) is 5.
- We have r(x)=3x−7
- We also have t(x)=3x+r(x)
- To find t(x), we substitute r(x) into the equation for t(x):
t(x)=3x+r(x)=3x+(3x−7)
- Combine like terms:
t(x)=3x+3x−7=6x−7
- Substitute x=2 into the simplified function t(x):
t(2)=6(2)−7
- Perform the multiplication and subtraction:
t(2)=12−7=5
Topper's Solved these Questions
- FUNCTIONS Book:KAPLANChapter:FUNCTIONS Exercise:FUNCTION NOTATION
Explore 1 Video
- FUNCTIONS Book:KAPLANChapter:FUNCTIONS Exercise:GRAPHS OF FUNCTIONS
Explore 1 Video
- FUNCTIONS Book:KAPLANChapter:FUNCTIONS Exercise:DESCRIBING REAL-LIFE SITUATIONS WITH FUNCTIONS
Explore 1 Video
- EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSBook:KAPLANChapter:EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSExercise:RATIONAL EXPRESSIONS AND EQUATIONS
Explore 1 Video
- GEOMETRY Book:KAPLANChapter:GEOMETRY Exercise:THREE-DIMENSIONAL FIGURES
Explore 1 Video
Similar Questions
Knowledge Check
If r=63x+2andtr=23s+2 ,what is the value of t?
A14B13C3D4f(x)=3x3−5x2−48x+80
If the zeros of function f defined above are represented by r, s, and t, what is the value of the sum r+s+t?A35B513C173D8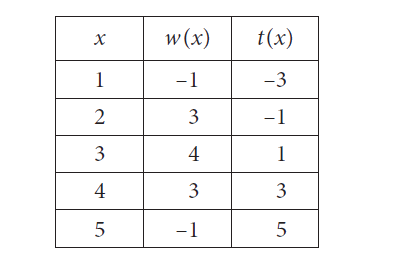
The table above shows some values of the functions w and t. For which value of x is w(x) + t(x) = x ?A1B2C3D4
The function f:R→R defined by f(x)=(x−1)(x−2)(x−3) is
View SolutionThe function f:R→R is defined by f(x)=(x−1)(x−2)(x−3) is
View SolutionThe function f:R→R defined as f(x)=3x2+3x−43+3x−4x2 is :
View SolutionThe function y=f(x) is defined by x=2t−|t|,y=t2+|t|,t∈R in the interval x∈[−1,1], then
View SolutionThe functions r is defined as g(x)=x23−|x−4|. For which values of x is g(x) NOT defined?
View Solution

