V=13π(d2)2h
A circle of rubber with a constant diameter d is placed on a table, its perimeter is anchored to the table and a string is attached to its centre. When the string is pulled upwards, a cone is formed with height h and volume V. The relationship between d, h, and V is represented above. Which of the following statements must be true ?
I. As the volume of the cone decreases, the height also decreases.
II. If the diameter of the base of the cone is 6 centimeters, the height can be determined by dividing the volume by 3π.
III. If the height of the conc triples, the volume must also triple.
I only
I and II only
II and III only
I, II, and III
The correct Answer is:D
To solve the problem, we need to analyze the given equation for the volume of the cone and evaluate the truth of each statement based on that equation.
Given Equation:
The volume V of the cone is given by:
V=13π(d2)2h
where d is the diameter of the base of the cone, and h is the height of the cone.
Step 1: Analyze Statement I
Statement I: As the volume of the cone decreases, the height also decreases.
Since the diameter d is constant, we can rewrite the equation as:
V=k⋅hwhere k=13π(d2)2
This shows that V is directly proportional to h. Therefore, if V decreases, h must also decrease.
Conclusion for Statement I: True.
Step 2: Analyze Statement II
Statement II: If the diameter of the base of the cone is 6 centimeters, the height can be determined by dividing the volume by 3π.
Let’s substitute d=6 cm into the volume equation:
V=13π(62)2h=13π⋅32⋅h=13π⋅9⋅h=3πh
To find h, we rearrange the equation:
h=V3π
Conclusion for Statement II: True.
Step 3: Analyze Statement III
Statement III: If the height of the cone triples, the volume must also triple.
From the volume equation:
V=k⋅h
If h triples (i.e., h becomes 3h), then:
V′=k⋅(3h)=3(k⋅h)=3V
This shows that if the height triples, the volume also triples.
Conclusion for Statement III: True.
Final Conclusion
Since all three statements are true, the correct answer is:
Option D: First, second, and third are all true.
The volume V of the cone is given by:
V=13π(d2)2h
where d is the diameter of the base of the cone, and h is the height of the cone.
Statement I: As the volume of the cone decreases, the height also decreases.
V=k⋅hwhere k=13π(d2)2
This shows that V is directly proportional to h. Therefore, if V decreases, h must also decrease.
Statement II: If the diameter of the base of the cone is 6 centimeters, the height can be determined by dividing the volume by 3π.
V=13π(62)2h=13π⋅32⋅h=13π⋅9⋅h=3πh
To find h, we rearrange the equation:
h=V3π
Statement III: If the height of the cone triples, the volume must also triple.
V=k⋅h
If h triples (i.e., h becomes 3h), then:
V′=k⋅(3h)=3(k⋅h)=3V
This shows that if the height triples, the volume also triples.
Since all three statements are true, the correct answer is:
Option D: First, second, and third are all true.
Topper's Solved these Questions
- LINEAR EQUATIONS AND GRAPHSBOOK - KAPLANCHAPTER - LINEAR EQUATIONS AND GRAPHSEXERCISE - SOLVING EQUATIONS
1 Videos
- LINEAR EQUATIONS AND GRAPHSBOOK - KAPLANCHAPTER - LINEAR EQUATIONS AND GRAPHSEXERCISE - WORD PROBLEMS
1 Videos
- LINEAR EQUATIONS AND GRAPHSBOOK - KAPLANCHAPTER - LINEAR EQUATIONS AND GRAPHSEXERCISE - LINEAR GRAPH
1 Videos
- INEQUALITIESBOOK - KAPLANCHAPTER - INEQUALITIESEXERCISE - MODELING REAL-LIFE SITUATIONS WITH INEQUALITIES
1 Videos
- PAIRED PASSAGES AND PRIMARY SOURCE PASSAGES BOOK - KAPLANCHAPTER - PAIRED PASSAGES AND PRIMARY SOURCE PASSAGES EXERCISE - HOW MUCH HAVE YOU LEARNED
11 Videos
Similar Questions
12(3X+14)=16(7X−10)
Which value of x satisfies the equation above ?
View SolutionA laser tag arean sells two types of memberships. One package costs $325 for one year of membership with an unilimated number of visits. The second package has a $125 enrollment fee, includes five free visits, and costs and additional $8 per visit after the first five. How many visits over a one-year period would a person who purchese the second package need to use for teh cost to equal that of the one-year membership ?
View SolutionWhat is the equation of the line that pases through the points (−3,1)and(1,3) ?
View SolutionTo make its sales goals for the month, a toy manufacture must sell at least $10,400 for of toy hoops and basketballs. Toy hoops sell for $8 and basketballs sell for $25. The company hopes to sell more than three times as many basketballs as toy hoops. If h represents the number of toy hoops and b represents the number of basketballs, where h and b are positive integer, which of the following systemsof inequalities best describes this situation ?
View SolutionPassage 1 is adapted from an 1823 speech by president james Monre, in which he discusses European colonialism in the Americas. The position expressed in this speech would eventually become known as the Monroe Doctrine. Passage 2 is adapted from a 1095 speech by President Theodore Roosevelt. His position would become known as the Roosevelt Corollary to the Monroe Doctrine.
Passage 1
The American continents, by the free and independent cnditin which they have assumed and maintain, are hence forth not to be considered as subjects for future colonization by any European powers. The citizens of the United States cherish friendaly sentiments in favor of teh liberty and happiness of their fellow men on the European side of the Atlantic. in the wars of the European powers in matters relating to themselves we have never taken any part, nor does it comport with out policy to do so. It is only when our rights are invarded or seriously menaced that we resent injuries or make preparatin for our defense. With the movements in our own hemisphere we are more immediately connected, by causes which must be obvious to all enlightened and impartial observers.
We owe it, therefore, to candor and to the amicable relations existing between the United States and European nations to declear that we should consider any attempt on their part to extend their system of government to any protion of this hemisphere as dangerous to our peace and safety. With the existing colonies or dependncies of any Wuropean powe we have not interfered and shall not interfere. however, we could not view any middling with those former European colonies who have declared their independence and maintained it, and whose independence we have, on great consideration and on just rinciples, acknowledged, in any other light than as the manifestation of an unfriendly desposition toward the united States.
Passage 2
It isw not true that the united States feels any land hunger or entertains any projects regarding the other nations of the Western Hemisphere except for their welfare. All that this country desires is to see our neighboring countries stable, orderly, and prosperous. Any country whose people conduct themselves well can count upon our hearty friendship. If a nation shows that it knows how to act with reasonalbe efficiency and decency in social and plitical matters, if it keeps order and pays its obligations, it need not fear interference from the United States. However, chronic wrongdoing, or an impotence which results in a general loosening of the ties of civilized society, may in America, as elsewhere, ultimately require intervention.... In thw Western Hempisphere, the adherence of the United States to the Monroe Doctrine may force the United States, however reluctantly, in flagrant cases of such wrongdoing or impotence, to the exercise of an inernational police power. If every country washed by the Caribbean Sea would show the progress in stable and just civilization which Cuba has shown since our troops left the island, and which so many of the republics in both Americas are constantly and brilliantly showing, all question of interference by this Nation with their affairs would be at an end. Our intersets and those of our southern neighbors are in reality identical. They have great natural riches, and if within their borders the reign of law and justice obtains, prosperity is sure to come to them. While they thus obey the primary laws of civilized society, they may rest assured that they will be treated by us in a spirit of cordial and helpful sympthy. We would interfere with them only in the last resort, and then only if it became evident that their inability or unwillingness to do justic at home and abroad had violated the rights of the United States or had invited foreign aggression to the determent of the entire body of American nations. Every nation, whether in America or anywhere else, which desires to maintain its freedom and independence must ultimately realize that the right of such independence can not be separated from the respondibility of making good use of it.
The primary purpose of the statement in lines 6-9 ("The citizens ...of the Atlantic") is to
View SolutionIf h,G,V,T are respectively the height,curved surface area,volume and total surface area of a cylinder,then prove that: V(pi h^(2)+C)+(V^(2))/(h)=h(T^(2))/(4)
View SolutionThe height h of cylinder equals the circumference of the cylinder. In terms of h, what is the volume of the cylinder? h34π (b) h22π (c) h32 (d) πh3
View SolutionIf the diameter of the base of a closed right circular cylinder be equal to its height h, then its whole surface area is
(a) 2πh2
(b) 32πh2
(c) 43πh2
(d) πh2
View SolutionWhen a rubber ball of volume v , bulk modulus K is at a depth h in water then decreases in its volume is
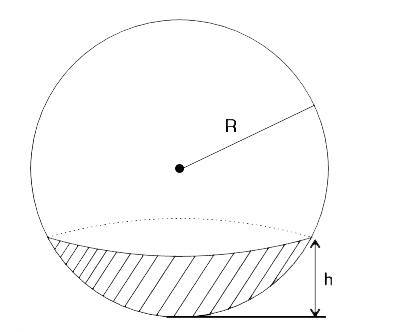
View SolutionShow that the volume of a segment of height h of a sphere of radius R is
V=13πh2(3R−h)
View Solutionयदि किसी शकु की ऊँचाई, वक्राठ और आयतन क्रमश: h , c और v हो, तो सिद्ध कीजिए की
3πvh3−c2h2+9v2=0
View SolutionVolume of cone with d as diameter and h as height is ……… units3.
View SolutionA cylinder has volume V, height h, and base diameter d. Which of the following represents d in terms of V and h?
View SolutionIf h,C,V represent height, curved surface area,
and volume of cone, prove that
3πVh3−C2h2+9V2=0.
View SolutionIf the height and radius of a cone of volume V are doubled, then the volume of the cone, is (a) 3 V (b) 4 V (c) 6 V (d) 8 V
View Solution
