Calculate the ratio of capacitance of two capacitors of same dimension of same dimensions but of different values K and $\frac{K}{4}$ arranged in two ways as shown in Fig. (i) and (ii).

$5 : 2$

$25 : 16$

$5 : 4$

$2 : 5$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Which of the two have same dimensions
AForce and strain
BForce and stress
CAngular velocity and frequency
DEnergy and strain
Which of the two have same dimensions ?
AForce and strain
BForce and stress
CAngular velocity and frequency
DEnergy and strain
The capacitance of a capacitor, filled with two dielectrics of same dimensions but of dielectric constants $K_{1} and K_{2}$ respectively as shown will be -
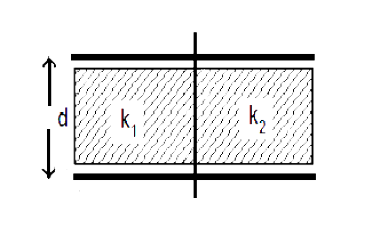A $\frac{\in_{0} A}{2 d} (K_{1} + K_{2})$
B $\frac{\in_{0} A}{d} (K_{1} + K_{2})$
C $\frac{\in_{0} A}{2 d} (\frac{K_{1} + K_{2}}{K_{1} + K_{2}})$
D $\frac{\in_{0} A}{d} (\frac{K_{1} K_{2}}{K_{1} + K_{2}})$