The moment of inertia of a system of four rods each of length l and mass m about the axis shown is
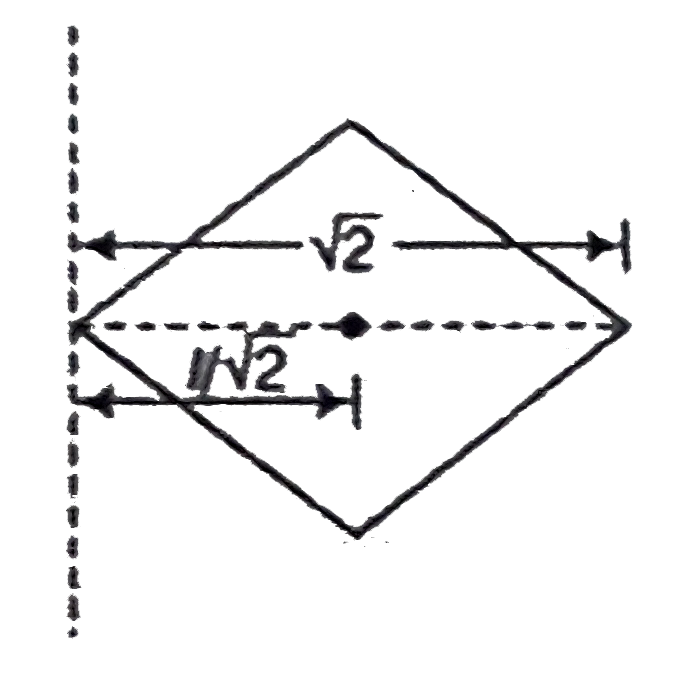
23ml2
2ml2
3 ml2
83ml2
d) Consider a square lamina, then
4m(l212+(l)212) about
Center of mass = 2ml23
Apply perpendicualr axes theorem
=2ml23+4m(l√2)2=83ml2

Topper's Solved these Questions
- ROTATIONAL MOTIONBook:BITSAT GUIDEChapter:ROTATIONAL MOTIONExercise:BITSAT Archives
Explore 9 Videos
- NEWTONS LAWS OF MOTION AND FRICTIONBook:BITSAT GUIDEChapter:NEWTONS LAWS OF MOTION AND FRICTIONExercise:BITSAT Archives
Explore 23 Videos
- SCALARS AND VECTORSBook:BITSAT GUIDEChapter:SCALARS AND VECTORSExercise:All Questions
Explore 34 Videos
Similar Questions
Knowledge Check
The moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an angle α is
 Aml23sin2αBml212sin2αCml22cos2αDml22cos2α
Aml23sin2αBml212sin2αCml22cos2αDml22cos2αThe moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L3 from one of its ends and perpendicular to the rod is
A7ML248BML29CML212DML23The moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L/3 from one of its ends and perpendicular to the rod is
A7ML248BML26CML29DML23
The moment of inertia of a thin uniform rod of mass M, length L, about an axis passing through its centre and making an angle θ with the rod is
View SolutionMoment of inertia of a uniform rod of length L and mass M , about an axis pasing through L/4 from one end and perpendicular to its length is
View SolutionMoment of inertia of a uniform rod of length L and mass M, about an axis passing through L/4 from one end and perpendicular to its length is
View SolutionThe moment of inertia of a thin uniform rod of mass M and length l about an axis perpendicular to the rod through its centre is I. The moment of inertia of the rod through its end point is
View SolutionThe moment of inertia of a thin uniform rod of mass M and length L about an axis perpendicular to the rod, through its centre is I. The moment of inertia of the rod about an axis perpendicular to rod through its end point is
View Solution


