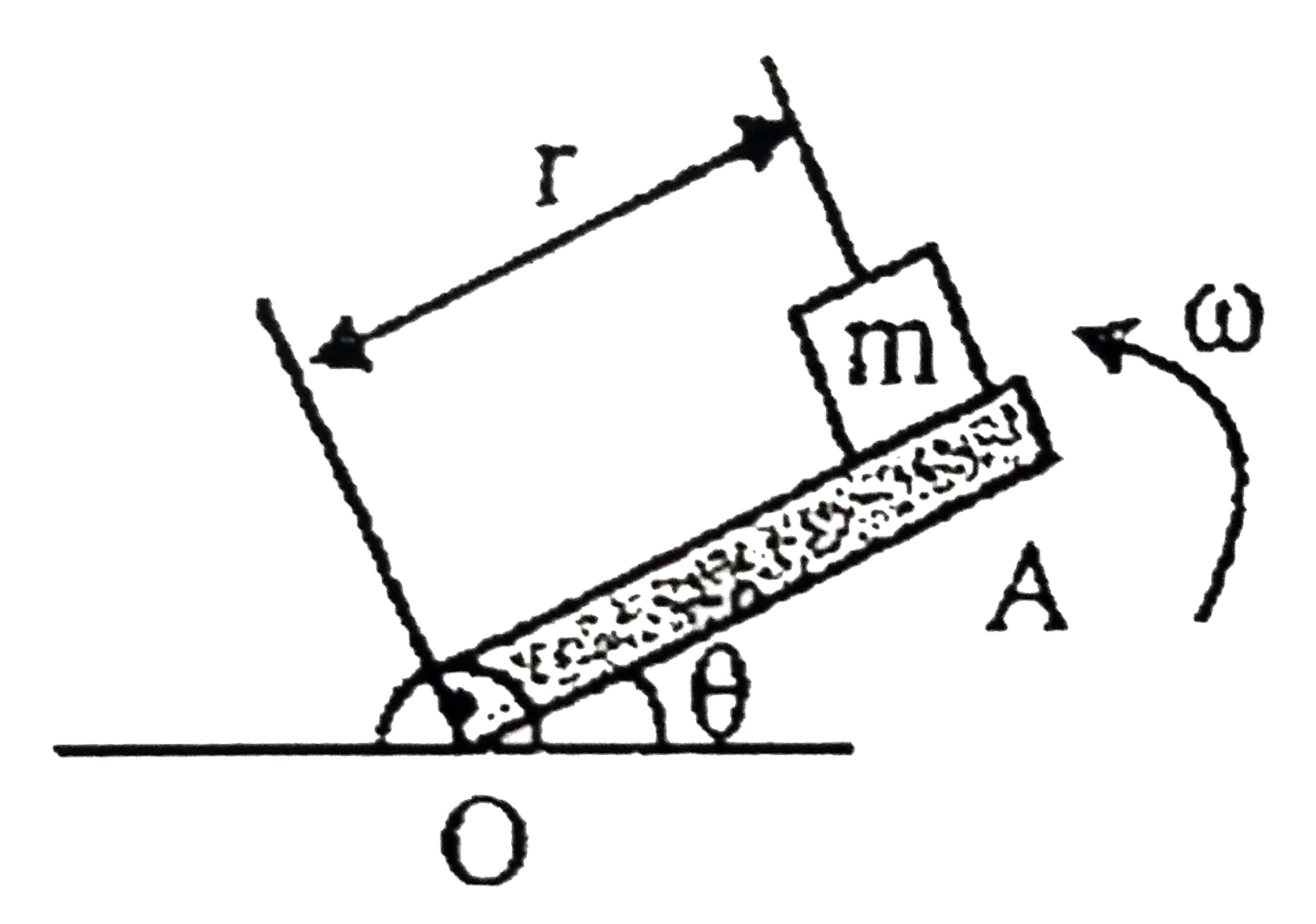
A rod OA rotates about a horizontal axis through O with a constant anti-clockwise velocity ω=3rad/s. As it pases the positions θ=0∘ a small block of mass m is placed on it at a radial distacne r=450 mm If the block is observed to slip at θ=50∘ the coefficient of static friction bewteen the block and the rod is (Given that ,sin50∘=0766,cos50∘=0.64)

0.2
0.55
0.8
1
(d) At the time of slipping maxnimum friction acts on the body
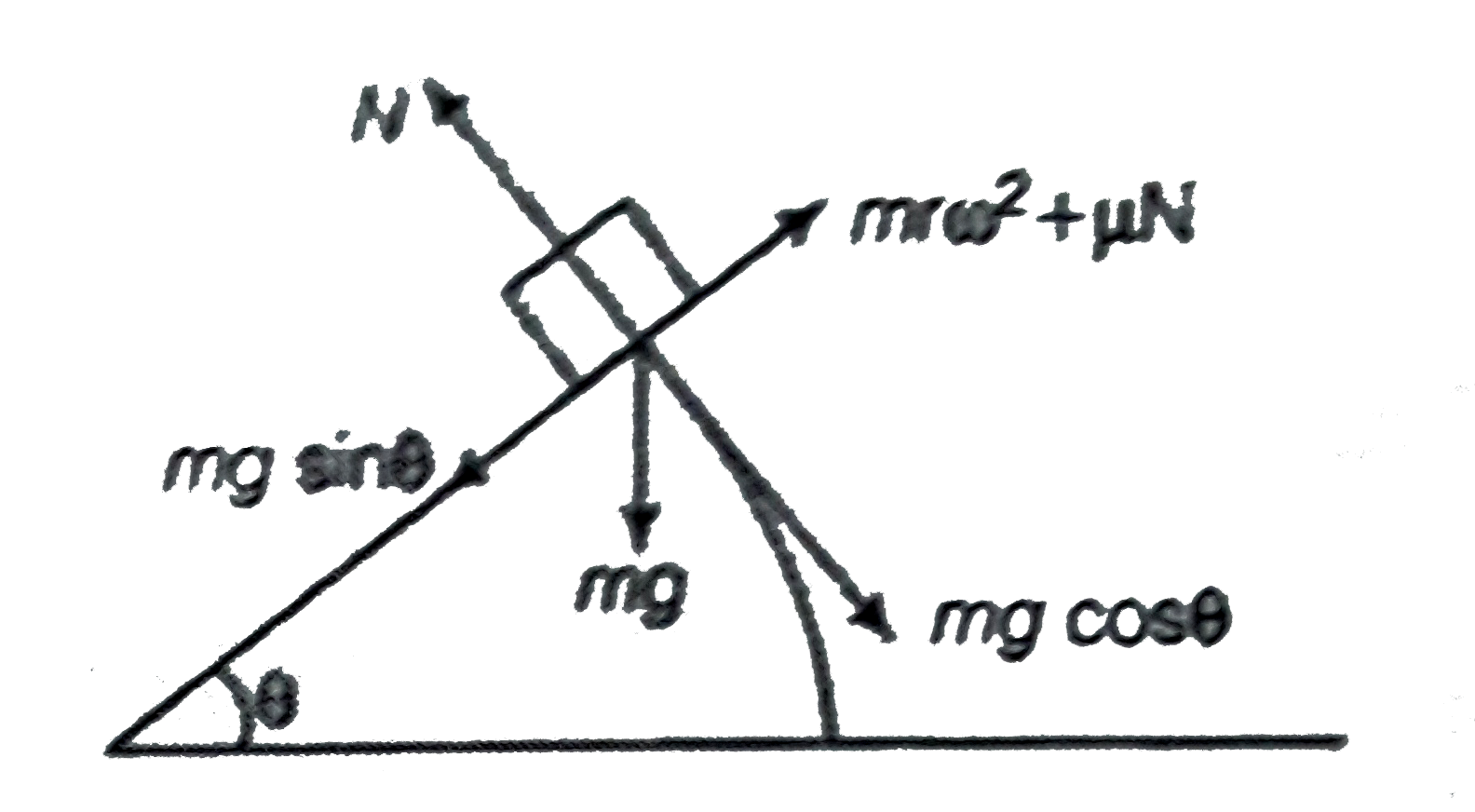
in the frame of rod,
mgsinθ=μN+mrω2
Also, " " N−mgcosθ
∴ mgsinθ=μmgcosθ+mrω2
Here, r=0.4.5m,θ=50∘
sin50∘=0.766and cos50∘=0.64
∴μ=mgsinθ−mrω2mgcosθ=gsinθ−rω22gcosθ=0.55
Topper's Solved these Questions
Similar Questions
A rod OA rotates about a horizontal axis through O with a constant aniclockwise velocity ω=3reds−1. As it passes the position θ=0, a small block of mass m is placed on it at a radial distance r=450mm if the block is observed to slip at θ=50∘ . Find the coefficient of static friction between the block and the rot
(Given that sin50∘=0.766,cos50∘=0.64)
View SolutionA wooden plank OA rotates in vertical plane about horizontal axis through O with a constant angular velocity ω=3rad/s . As it passes the position θ=0 , a small mass m is placed upon it at a radial distance r=0⋅5 m . If the mass m starts sliding at θ=37∘ , find the coefficient of friction between mass and the plane .
View Solution
Knowledge Check
A block of mass 50 kg slides over a horizontal distance of 1m. If the coefficient of friction between their surface is 0.2, then work done against friction is (take g=9.8m/s2) :
A98 JB72 JC56 JD34 J
The inclined plane OA rotates in vertical plane about a horizontal axis through O with a constant counter clockwise velocity ω=3 rad/sec. As it passes the position θ=0, a small m=1 kg is placed upon it at a radial distance r=0.5 m. if the mass is observed to be at rest with respect to inclined plane. The value of static friction force at θ=37∘ between the mass and the incline plane
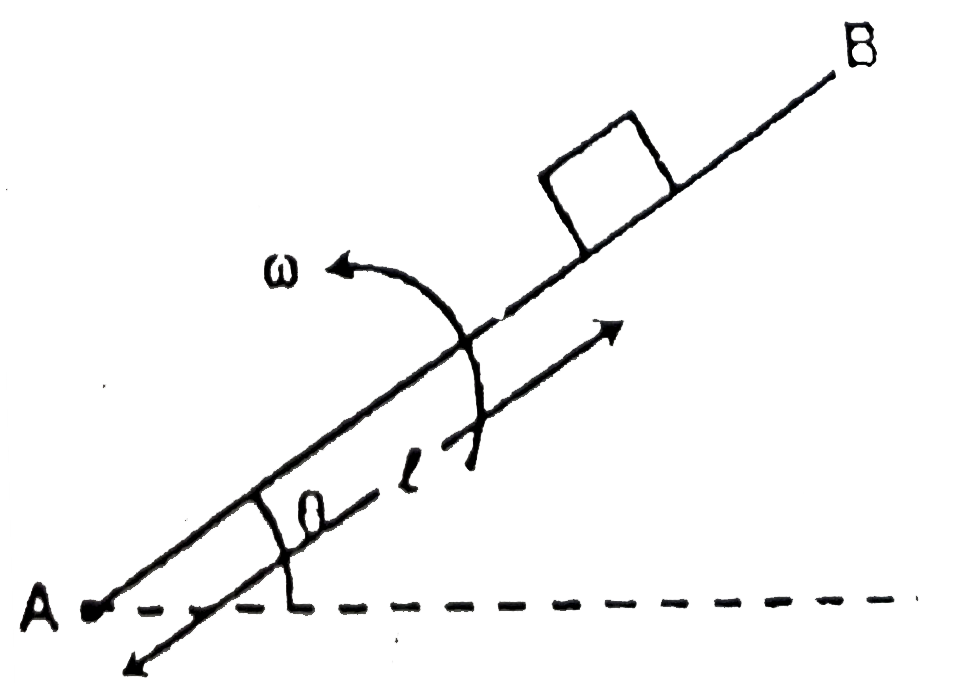
View SolutionA plank is rotating in a vertical plane about one of its ends with a constant angular velocity ω=√2rad/s. A block of mass m=2kg is placed at a distance l=1m from its end A (see figure) which is hinged. The block starts sliding down when the plank makes an angle θ=30∘ with the horizontal. If coefficient of friction between the plank and the block is μ and given that μ2=k/25. Find the value of k.
View SolutionA homogeneous disc of weight W and radius R rotates about the vertical axis OZ, the initial angular velocity being ω0. During the motion, the brake block A is pressed to the disc,with a radial force N for t0 seconds and the disc comes to rest because of friction. Find the coefficient of friction.
View SolutionA cubical block of mass M vibrates horizontally with amplitude of 4.0 cm and a frequency of 2.0 Hz. A small block of mass is placed on the bigger block. In order that the smaller block does not side on the bigger block, the minimum value of the coefficient of static friction between the two blocks is (0.16x). Find the valule of x(Take π2=10 and g=10m/s2)
View SolutionA disc of radius 4m is rotating about its fixed centre with a constant angular velocity 2rads (in the horizontal plane).A block is also rotating with the disc without slipping. If co-efficient of friction between the block and the disc is 0.4 ,then the maximum distance at which the block can rotate without
View SolutionA rod AB of length 2m is hinging at point A and its other end B is attached to a platform on which a point of mass m is kept. Rod rotates about point A maintain angle θ=30∘ with the vertical in such a way that platform remain horizontal and revolves on the horizontal circular path. If the coefficient of static friction between the block and platform is μ=0.1 then find the maximum angular velocity in rads−1 of rod so that the block does not slip on the platform (g=10ms−2)
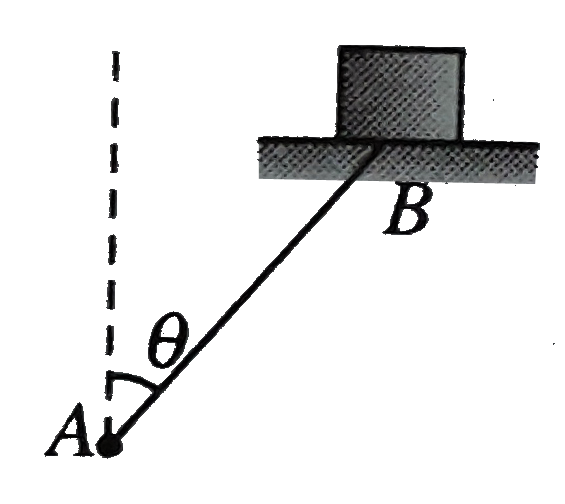
View SolutionA block of mass m is kept on the edge of a horizontal turn table of radius R which is rotating with constant angular verticle ω (along with the block ) about its axis . If coefficient of friction is μ, find the friction force between block and table.
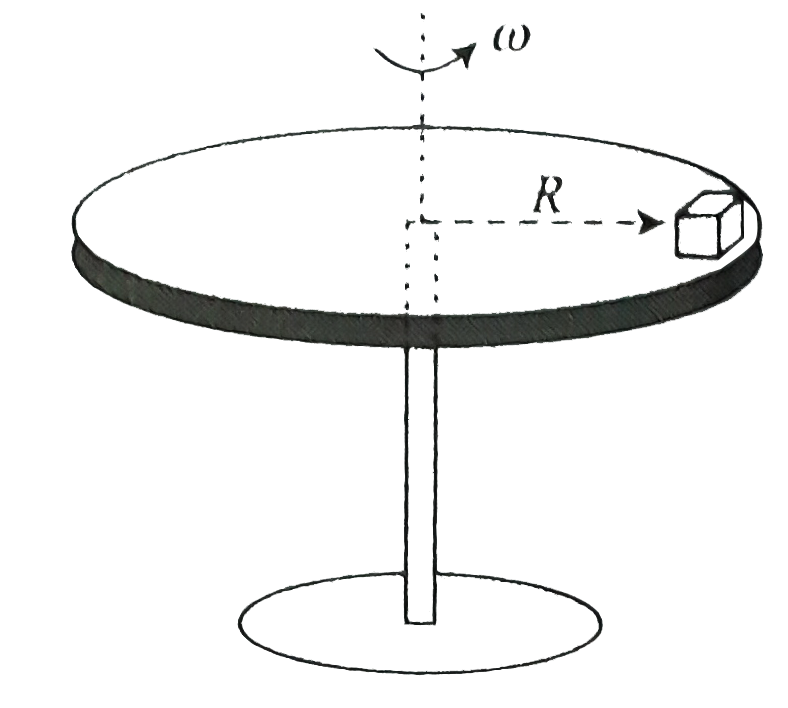
View Solution
