A wooden plank OA rotates in vertical plane about horizontal axis through O with a constant angular velocity ω=3rad/s . As it passes the position θ=0 , a small mass m is placed upon it at a radial distance r=0⋅5 m . If the mass m starts sliding at θ=37∘ , find the coefficient of friction between mass and the plane .
To find the coefficient of friction between the mass m and the wooden plank as it rotates, we can follow these steps:
Step 1: Understand the forces acting on the mass
When the mass m is placed on the rotating plank, it experiences gravitational force mg acting downwards, and a normal force N acting perpendicular to the surface of the plank. Additionally, there is a frictional force f acting along the surface of the plank.
Step 2: Set up the equations of motion
At an angle θ=37∘, the forces can be resolved into components:
- The gravitational force can be resolved into two components:
- mgcosθ acting perpendicular to the plank (which is balanced by the normal force N)
- mgsinθ acting parallel to the plank (which causes the mass to slide)
The centripetal force required to keep the mass moving in a circular path is provided by the net force acting towards the center of the circular path.
Step 3: Write the equations
1. The normal force N is given by:
N=mgcosθ
2. The frictional force f can be expressed as:
f=μN=μmgcosθ
3. The net force acting towards the center of the circular path is:
Fnet=mgsinθ−f
This net force must equal the required centripetal force, which is given by:
Fcentripetal=mv2r
where v=ωr and ω is the angular velocity.
Step 4: Substitute and simplify
Using v=ωr:
Fcentripetal=m(ωr)2r=mω2r
Setting the net force equal to the centripetal force:
mgsinθ−μmgcosθ=mω2r
Step 5: Cancel mass m and rearrange
Dividing through by m (assuming m≠0):
gsinθ−μgcosθ=ω2r
Rearranging gives:
μgcosθ=gsinθ−ω2r
Step 6: Solve for the coefficient of friction μ
μ=gsinθ−ω2rgcosθ
Step 7: Substitute known values
Given:
- g=9.81m/s2
- θ=37∘
- ω=3rad/s
- r=0.5m
Calculating sin37∘ and cos37∘:
- sin37∘≈0.6
- cos37∘≈0.8
Now substituting these values:
μ=9.81×0.6−(32×0.5)9.81×0.8
Calculating:
μ=5.886−4.57.848=1.3867.848≈0.176
Final Answer
The coefficient of friction μ is approximately 0.176.
---
When the mass m is placed on the rotating plank, it experiences gravitational force mg acting downwards, and a normal force N acting perpendicular to the surface of the plank. Additionally, there is a frictional force f acting along the surface of the plank.
At an angle θ=37∘, the forces can be resolved into components:
- The gravitational force can be resolved into two components:
- mgcosθ acting perpendicular to the plank (which is balanced by the normal force N)
- mgsinθ acting parallel to the plank (which causes the mass to slide)
1. The normal force N is given by:
N=mgcosθ
f=μN=μmgcosθ
Fnet=mgsinθ−f
This net force must equal the required centripetal force, which is given by:
Fcentripetal=mv2r
where v=ωr and ω is the angular velocity.
Using v=ωr:
Fcentripetal=m(ωr)2r=mω2r
mgsinθ−μmgcosθ=mω2r
Dividing through by m (assuming m≠0):
gsinθ−μgcosθ=ω2r
μgcosθ=gsinθ−ω2r
μ=gsinθ−ω2rgcosθ
Given:
- g=9.81m/s2
- θ=37∘
- ω=3rad/s
- r=0.5m
- sin37∘≈0.6
- cos37∘≈0.8
μ=9.81×0.6−(32×0.5)9.81×0.8
μ=5.886−4.57.848=1.3867.848≈0.176
The coefficient of friction μ is approximately 0.176.
Topper's Solved these Questions
- LAWS OF MOTIONBook:AAKASH INSTITUTEChapter:LAWS OF MOTIONExercise:Illustration
Explore 5 Videos
- LAWS OF MOTIONBook:AAKASH INSTITUTEChapter:LAWS OF MOTIONExercise:TRY YOURSELF
Explore 67 Videos
- KINETIC THEORYBook:AAKASH INSTITUTEChapter:KINETIC THEORYExercise:EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
Explore 10 Videos
- MAGNETISM AND MATTER Book:AAKASH INSTITUTEChapter:MAGNETISM AND MATTER Exercise:ASSIGNMENT (SECTION D)
Explore 26 Videos
Similar Questions
A rod OA rotates about a horizontal axis through O with a constant aniclockwise velocity ω=3reds−1. As it passes the position θ=0, a small block of mass m is placed on it at a radial distance r=450mm if the block is observed to slip at θ=50∘ . Find the coefficient of static friction between the block and the rot
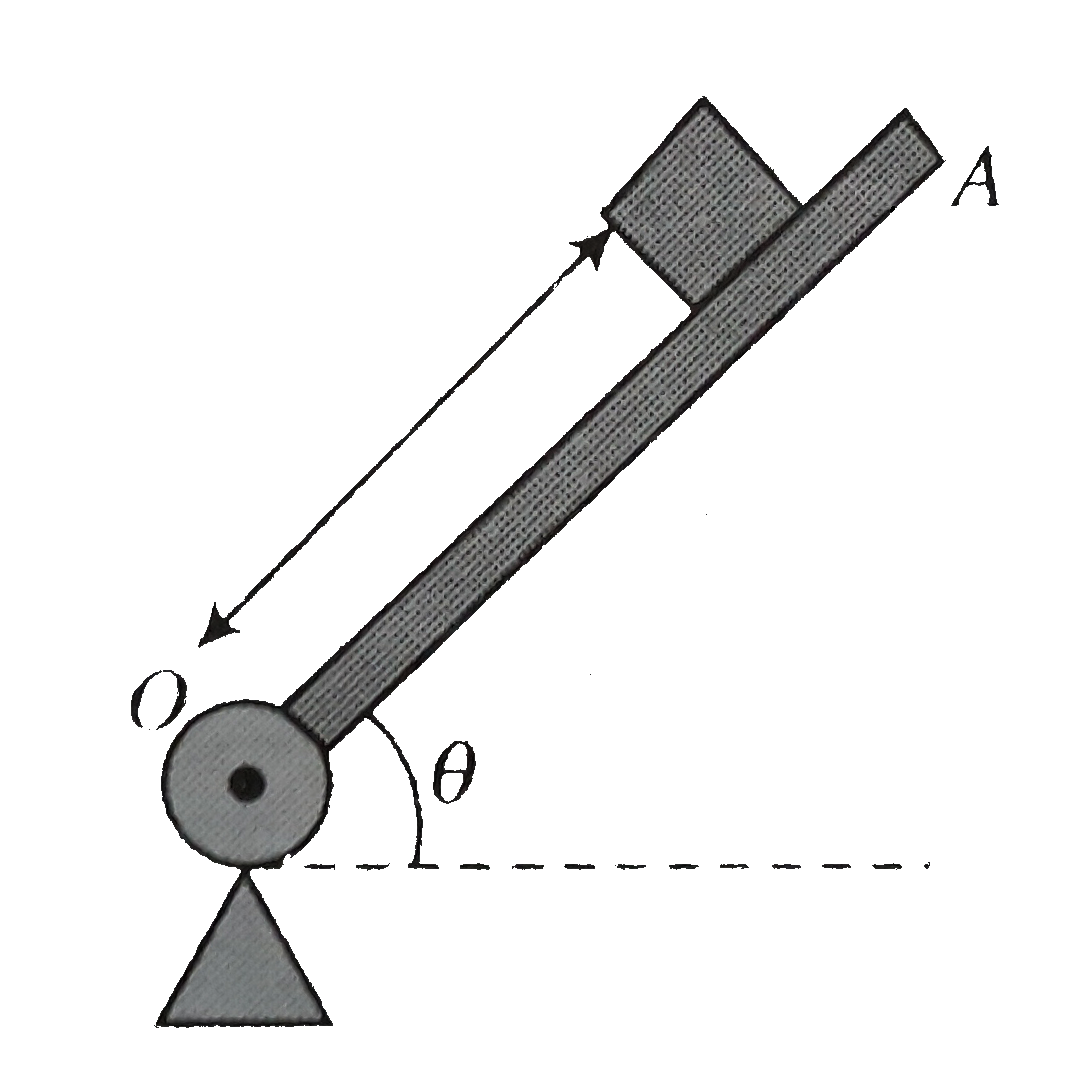
(Given that sin50∘=0.766,cos50∘=0.64)
View SolutionThe inclined plane OA rotates in vertical plane about a horizontal axis through O with a constant counter clockwise velocity ω=3 rad/sec. As it passes the position θ=0, a small m=1 kg is placed upon it at a radial distance r=0.5 m. if the mass is observed to be at rest with respect to inclined plane. The value of static friction force at θ=37∘ between the mass and the incline plane
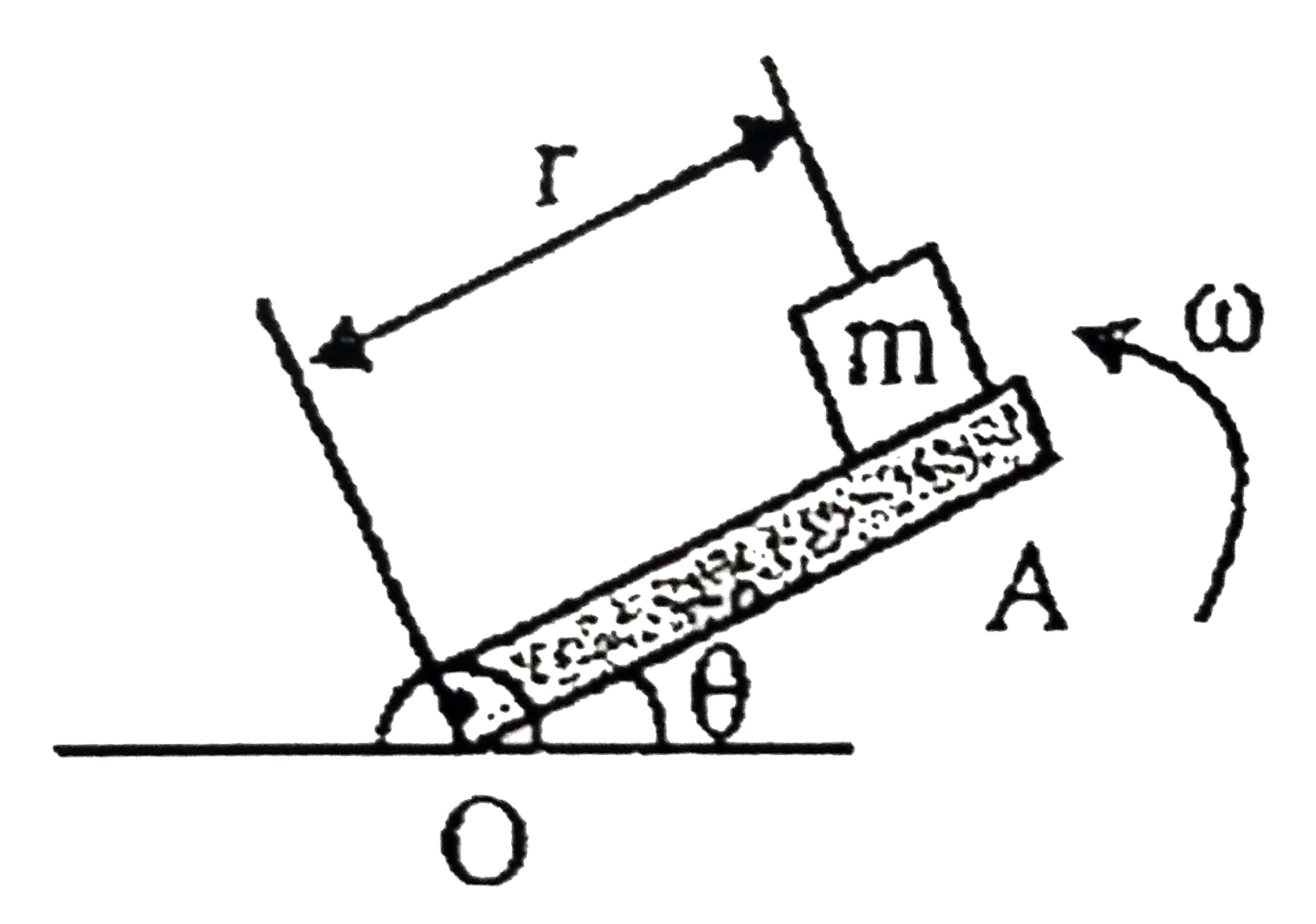
View Solution
Knowledge Check
A rod OA rotates about a horizontal axis through O with a constant anti-clockwise velocity ω=3rad/s. As it pases the positions θ=0∘ a small block of mass m is placed on it at a radial distacne r=450 mm If the block is observed to slip at θ=50∘ the coefficient of static friction bewteen the block and the rod is (Given that ,sin50∘=0766,cos50∘=0.64)
 A0.2B0.55C0.8D1
A0.2B0.55C0.8D1A ring of radius r is rotating about a vertical axis along its diameter with constant angular velocity ω.A read of mass m remains at rest w.r.t. ring at the position shown in figure. Then w2 is:
_2019_CBT8_E01_015_Q01.png) Ag√3B2g√3rC√3grDgr
Ag√3B2g√3rC√3grDgr
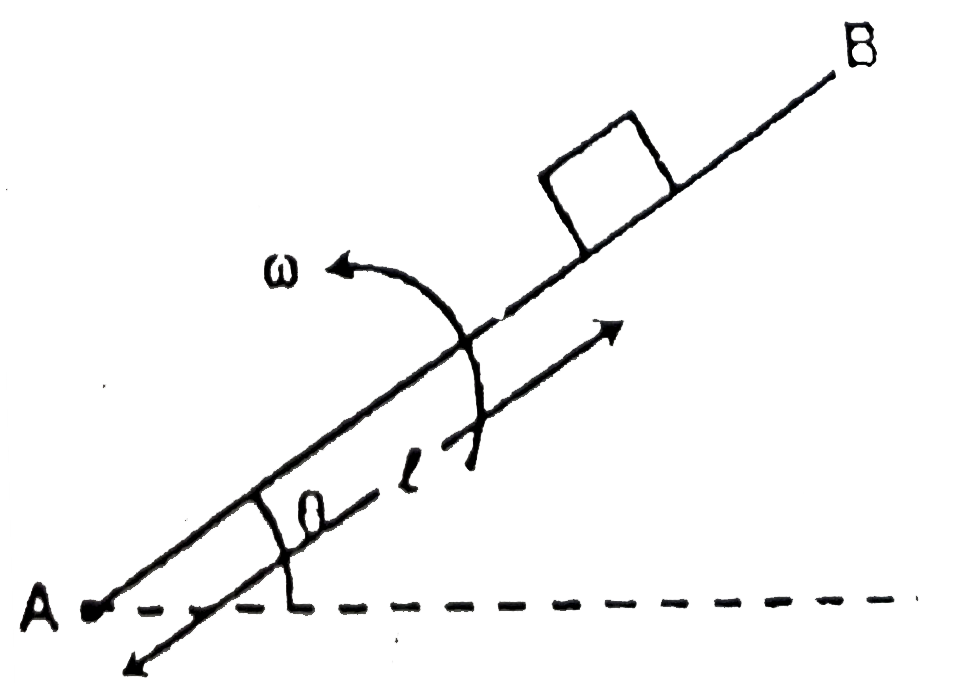
A plank is rotating in a vertical plane about one of its ends with a constant angular velocity ω=√2rad/s. A block of mass m=2kg is placed at a distance l=1m from its end A (see figure) which is hinged. The block starts sliding down when the plank makes an angle θ=30∘ with the horizontal. If coefficient of friction between the plank and the block is μ and given that μ2=k/25. Find the value of k.
View SolutionA solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity ω. Its K.E. Is
View SolutionA ring of mass m and radius R is being rotated about its axis with constant angular velocity ω in the gravity free space. Find tension in the ring.
View SolutionA small block of mass m is placed at a distance r from one end of a plank. The plank is given a constant angular velocity ω about an axis passing through point O and perpendicular to the plane. The block starts sliding down the plane when the plank makes an angle θ with horizontal. Calculate the coefficient of friction between the particle and the plank.
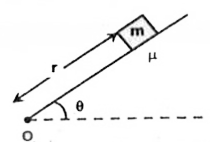
View Solution
A rod of mass 2 kg ad length 2 m is rotating about its one end O wth an angular velocity ω=4rad/s. Find angular momentum of the rod about the axis rotation.
View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity ω. If a increases then tension in ring
View Solution

